Dérivée de 4/ racine de (x²+4)
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Isam93
- Messages: 5
- Enregistré le: 14 Mar 2010, 15:20
-
 par Isam93 » 14 Mar 2010, 15:25
par Isam93 » 14 Mar 2010, 15:25
Bonjour à tous,
Alors voilà ça fait plusieurs heures que j'essaye de trouver la dérivée de cette fonction mais sans succès, je trouve des résultats super chargés avec plein de divisions, alors si quelqu'un pourrait m'aider ça serait pas mal,
merci :zen:
-
Billball
- Membre Complexe
- Messages: 2669
- Enregistré le: 31 Mar 2006, 19:13
-
 par Billball » 14 Mar 2010, 15:26
par Billball » 14 Mar 2010, 15:26
salut,
écris 4* 1/u
avec u = (x²+4)^0.5
pis la dérivé de 1/u tu connais ..
-
Isam93
- Messages: 5
- Enregistré le: 14 Mar 2010, 15:20
-
 par Isam93 » 14 Mar 2010, 15:35
par Isam93 » 14 Mar 2010, 15:35
Merci pour cette réponse rapide, donc si je comprend bien, ça nous donne
u(x)=4 u'(x)=0
v(x)= 1/(x²+4)^0.5 v'(x)= -1/x²+4
??
-
Billball
- Membre Complexe
- Messages: 2669
- Enregistré le: 31 Mar 2006, 19:13
-
 par Billball » 14 Mar 2010, 15:40
par Billball » 14 Mar 2010, 15:40
bah 4 tu t'enfous car c'est une constante donc
 = 4 \times \frac{1}{\sqrt{x^2 + 4}})
donc
 = 4 \times u(x))
avec :
 = \frac{1}{\sqrt{x^2 + 4}})
u'(x) =
et sinon
(1/u)' = -u'/u²
-
Isam93
- Messages: 5
- Enregistré le: 14 Mar 2010, 15:20
-
 par Isam93 » 14 Mar 2010, 16:05
par Isam93 » 14 Mar 2010, 16:05
La dérivée est alors -4/(x²+4) ?

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 14 Mar 2010, 16:10
par Ericovitchi » 14 Mar 2010, 16:10
non tu as oublié le u'. Ca va te créer un 2x en plus
-
Isam93
- Messages: 5
- Enregistré le: 14 Mar 2010, 15:20
-
 par Isam93 » 14 Mar 2010, 16:14
par Isam93 » 14 Mar 2010, 16:14
Je comprend pas le 2x en plus ?

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 14 Mar 2010, 16:25
par Ericovitchi » 14 Mar 2010, 16:25
tu as dérivé comme un 2/u avec u =
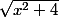
la dérivée vaut -2u'/u² donc il faut bien calculer u' la dérivée de la racine
c'est de la forme

donc la dérivée vaut

donc
=x/\sqrt{x^2+4})
donc en tout ça va te faire -2u'/u²=
\sqrt{x^2+4})
-
Isam93
- Messages: 5
- Enregistré le: 14 Mar 2010, 15:20
-
 par Isam93 » 14 Mar 2010, 16:30
par Isam93 » 14 Mar 2010, 16:30
Merci j'ai enfin saisi le truc après tant d'essais sur mon brouillon
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 138 invités
