Sev supplémentaires

[polkadots]

Bonjour,

Je viens de commencer les espaces vectoriels, et à vrai dire, même si jconnais le cours, j'ai du mal avec les exos. J'ai ici la correction d'une "application" mais je ne vois pas en quoi on a pu "montrer le résultat".

Dans 4, prouver que les sev F et G sont supplémentaires où F= (1,0,0,1) et G={(x,y,z,t) R4 / x+y+z+t=0}.

J'ai compris comment montrer que F+G = R4. Par contre, on me dit qu'il suffit de montrer que la famille est libre pour que F et G soient supplémentaires, car:

lambda(1,0,0,1) - mu(1,0,0,-1) + beta(0,1,0,-1) + delta(0,0,1,-1) = (0,0,0,0)

Donc il faut montrer que tous les scalaires sont nuls et que les vecteurs sont linéairements indépendants.

Sauf qu'ils me mettent en guise de conclusion: "Le vecteur appartenant à ces deux espaces est nul, donc l'intersection de F et G est = {0,0,0,0}...


N'auriez-vous pas une autre méthode pour résoudre cet exo? Ou alors pourriez-vous m'expliquer en quoi on a montré qu'ils étaient supplémentaires?

[Doraki]

On a F = {(x,0,0,x), x dans R} et G = {(x,y,z,t) / x+y+z+t = 0}.

Tu veux dire que pour montrer que leur intersection est nulle ils ont fait autre chose que "x+0+0+x = 0 <=> 2x = 0 <=> x=0" ?

[Finrod]

Ils disent que vérifier que l'intersection de F et G est nulle est facile.

Pour cela il suffit de voir que (1,0,0,1) n'est pas dans G, ce qui est clair puisque pour ce vecteur la somme des coef fait 2 et non 0.

Après, F et G sont supplémentaires dans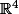 si et seulement si deux des trois points suivants sont vérifiés :

1 - intersection nulle.
2 - Somme =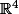
3 - Somme des dimension égale à 4.

Ici le plus rapide est d'utiliser la somme des dimensions et l'intersection nulle.

[polkadots]

Ah oui, suis-je bète.... Merci!!

[polkadots]

Comment montriez-vous que la somme des dimensions est égale à 4? Je viens tout juste de commencer ce cours, alors niveau application c'est pas top...

Enfin comment déterminer la dimension de F et celle de G?

[Ben314]

La dimension d'un s.e.v. G, c'est le nombre d'élément d'une base de G, c'est à dire d'une famille libre et génératrice de G.

Par définition de F, la famille {(1,0,0,1)} est génératrice de F et elle est évidement libre (une famille formée d'un seul vecteur non nul est forcément libre) donc dim(F)=1.

Pour E, c'est un peu plus long (surtout si tu débute avec les espaces vectoriels).
Tu écrit que (x,y,z,t) est dans E ssi t=-x-y-z c'est à dire ssi
(x,y,z,t)=x(1,0,0,-1)+y(0,1,0,-1)+z(0,0,1,-1).
Cela prouve que la famille {(1,0,0,-1), (0,1,0,-1), (0,0,1,-1)} est génératrice de E, et tu fait la vérif usuelle pour montrer qu'elle est libre (c'est complètement évident ici). Donc dim(E)=3

[polkadots]

Je ne comprends pas pourquoi Dim(F)=1?

Vous dites que si une famille comporte au moins un vecteur non nul, elle est forcément libre? et là elle en comporte 2

[Ben314]

Ben....
Il me semble que la famille { (1,0,0,1) } ne comporte bien qu'un seul vecteur...
Je ne comprendd pas où tu en vois un deuxième (si c'est le fait que cet unique vecteur a deux coordonnées non nulles, cela n'a absolument rien à voir avec le problème : ce que l'on compte, c'est le nombre de vecteurs...)

P.S. si le "vous" s'adresse à moi, tu oublie...

[polkadots]

je te remercies, jcomprends bien mieux..!

[Doraki]

Sinon, c'est pas très difficile de montrer que la somme de F et G fait R^4.

On veut montrer que tout vecteur u de R^4 sécrit v+w avec v dans F (donv v = a*(1,0,0,1)) et w dans G.

La description que tu as de G fait que c'est super facile de vérifier qu'un vecteur est dans G.
Donc le plus simple est de trouver le réel a tel que le vecteur v - a*(1,0,0,1) soit dans G.
Si pour tout v tu trouves un a tel que v-a*(1,0,0,1) est dans G, tu auras montré que R^4 = F+G.

[Ben314]

Je "plussois" par rapport à ce que dit doraki.

Tu constate qu'il y a de multiples méthodes pour montrer le résultat.
Ce qui est important c'est le post de Finrod : sur les trois propriétés, il suffit d'en montrer 2 et il est souvent malin de choisir les deux plus simples.

Le calcul des deux dimensions (dim(E)=3 et dim(F)=1) permet de montrer la propriété 3 de Finrod.

L'idée de doraji est de montrer plutôt le 2 de Finrod (c'est un peu plus court)

Et, tout le monde est d'accord sur le fait que dans cet exercice, le 1 de finrod est évident.

Il faut aussi comprendre que, si tu montre que 2 des trois sont vrai alors cela implique que la troisième est aussi vrai.

Donc, pour la preuve, tu choisi : soit tu prouve 1 et 2 (et tu en déduit que 3 est vrai) soit tu prouve 1 et 3 (et tu en déduit que 2 est vrai)