Somme de puissances des entiers
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
 par metamasterplay » 19 Déc 2009, 15:29
par metamasterplay » 19 Déc 2009, 15:29
Bonjours,
un exercice sur les récurrences que j'ai trouvé et que je n'arrive pas à résoudre:
Soit P un polynôme de degré k, montrer qu'il existe un polynôme de degré K+1 tel que:
[CENTER]
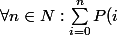=Q(n))
[/CENTER]
Pour y arriver il me faut démontrer que la somme jusqu'à un certain n des k-puissances des entiers est un polynôme en n de degré K+1, i.e:
[CENTER]
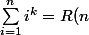 / deg(R)=k+1)
[/CENTER]
Une formule un peu familière qu'on trouve souvent pour les premières puissances:
[CENTER]
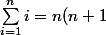/2)
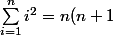(2n+1)/6)
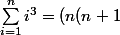/2)^2)
[/CENTER]
Mais je n'arrive pas à trouver une formule générale :triste: .
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 19 Déc 2009, 15:40
par girdav » 19 Déc 2009, 15:40
Salut!
Tu peux développer
^i)
par le binôme de Newton et sommer sur

.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 19 Déc 2009, 15:57
par Ben314 » 19 Déc 2009, 15:57
Salut,
Pour trouver le polynôme Q (de ta première question), tu écrit que Q doit vérifier ??? pour que l'on puisse montrer (par récurrence sur n) que la formule qui t'interesse est vraie.
Ensuite tu écrit Q(x)=a_0+a_1X+...+a_(k+1)X^k et tu regarde le système d'équations (linéaires) que cela donne. Il est clair que ce système admet une et une seule solution...
P.S. : La méthode proposée par Girdav est légèrement différente et permet d'expliquer pourquoi il existe des formules similaires au 3 que tu as donné (et même de les calculer de proche en proche...)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 47 invités
