Sommes des puissances des entiers
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 13 Sep 2009, 23:46
par Nightmare » 13 Sep 2009, 23:46
Salut à tous :happy3:
Un topic posté aujourd'hui sur la somme des n premiers cubes m'a fait réfléchir au problème suivant :
Quels sont les triplets d'entiers (a,b,c) tels que
^{c})
?
J'ai trouvé une solution plutôt simple, je vous laisse réfléchir au problème si ça vous tente.
:happy3:
-
le_fabien
- Membre Complexe
- Messages: 2737
- Enregistré le: 05 Oct 2007, 10:00
-
 par le_fabien » 14 Sep 2009, 05:08
par le_fabien » 14 Sep 2009, 05:08
Salut,
je me souviens que la somme des cubes des n premiers entiers est égal au carré de la somme des n premiers entiers. :zen:
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 14 Sep 2009, 11:12
par Nightmare » 14 Sep 2009, 11:12
Salut !
Oui, c'est une formule bien connue. La question est de savoir s'il y en a d'autres !
-
grandanois
- Membre Naturel
- Messages: 11
- Enregistré le: 03 Sep 2009, 16:13
-
 par grandanois » 14 Sep 2009, 11:27
par grandanois » 14 Sep 2009, 11:27
[FONT=Times New Roman]
ce possible factorisation ( summation, analogue a integration, derivation est substitue avec operateurs de difference (Delta)
a facteurs .. ... fa1^c...facb^c (b*c facteurs)
----------- = -------------------
.... a! ............ ..... (b!)^c
les denominateures peut-e^tre son different.
ce marche ?
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 14 Sep 2009, 11:28
par Nightmare » 14 Sep 2009, 11:28
Désolé mais je n'ai pas compris grand chose à ton message.
-
grandanois
- Membre Naturel
- Messages: 11
- Enregistré le: 03 Sep 2009, 16:13
-
 par grandanois » 14 Sep 2009, 11:37
par grandanois » 14 Sep 2009, 11:37
la somme de k eleve a =
nominateur= a+1 facteuers denominateur (a+1)! (correction ce a+1 analoge a intergration.)
summation, analogue a integration, derivation est substitue avec operateurs de difference (Delta)., ce inclue les numeros de Bernulli
beaucoup de travaille.
reviendre plus tarde
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 14 Sep 2009, 12:34
par girdav » 14 Sep 2009, 12:34
Bonjour.
Je ne sais pas si les relations suivantes vont servir:
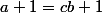)
et
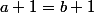^c)
.
Après je comptais considérer les différents cas de parité:

a la même parité que
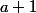
et que

.
-
le_fabien
- Membre Complexe
- Messages: 2737
- Enregistré le: 05 Oct 2007, 10:00
-
 par le_fabien » 14 Sep 2009, 12:38
par le_fabien » 14 Sep 2009, 12:38
grandanois a écrit:la somme de k eleve a =
nominateur= a+1 facteuers denominateur (a+1)! (correction ce a+1 analoge a intergration.)
summation, analogue a integration, derivation est substitue avec operateurs de difference (Delta)., ce inclue les numeros de Bernulli
beaucoup de travaille.
reviendre plus tarde
Bonjour grandanois,
tu vies où ? Dans quel pays ? :zen:
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 14 Sep 2009, 12:41
par Nightmare » 14 Sep 2009, 12:41
Girdav > Oui tu obtiens les bonnes relations! Puis-je avoir ta démarche?
Sinon la conclusion est très proche, je te laisse terminer.
:happy3:
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 14 Sep 2009, 12:46
par girdav » 14 Sep 2009, 12:46
En fait je raisonne pour la première sur les degré, et pour la seconde sur les coefficients dominants.
En posant
 =\Bigsum_{k=1}^n k^j)
on peut montrer par récurrence sur

(via le binôme de Newton) que
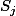
est un polynôme en

de degré
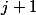
, et même travail (ça doit se faire en même temps) pour le coefficient dominant (qui vaut

). On l'élève à la puissance

pour
\)^c)
.
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 14 Sep 2009, 12:59
par Nightmare » 14 Sep 2009, 12:59
Intéressant ! Je n'ai pas fait ainsi, mon idée était simplement de raisonner sur des équivalents pour n -> oo.
-
skilveg
- Membre Relatif
- Messages: 462
- Enregistré le: 21 Mai 2008, 21:29
-
 par skilveg » 14 Sep 2009, 14:14
par skilveg » 14 Sep 2009, 14:14
Oui mais c'est strictement équivalent, pour des polynômes...
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 14 Sep 2009, 14:21
par Nightmare » 14 Sep 2009, 14:21
Oui oui ça revient au même mais c'est beaucoup plus rapide ainsi (on fait apparaitre une somme de Riemann et hop)
-
skilveg
- Membre Relatif
- Messages: 462
- Enregistré le: 21 Mai 2008, 21:29
-
 par skilveg » 15 Sep 2009, 05:11
par skilveg » 15 Sep 2009, 05:11
Je suis bien d'accord.
-
grandanois
- Membre Naturel
- Messages: 11
- Enregistré le: 03 Sep 2009, 16:13
-
 par grandanois » 15 Sep 2009, 09:31
par grandanois » 15 Sep 2009, 09:31
CORRECTION:
Bonjour le fabien.
Grandanois, = le chein du Danemark, je vive au Danemark et Uruguay.
où sont les signe de Latex?
la sommme k^a = (B a+1(n+1) - B a+1(1))/(a+1) "le primitive" eleve exponent +1 y diviision avec a+1. comme un primitive normal.
B a+1(n) =polinomi de Bernulli grad = a
L.es nuemro a de Bernulli = B a(0)
Pour deduce cette , if faut etudie SUmmation finte(j´écrie 5 pagine , vous me envie un email amaliegade40Agmail.com.)
la metode es aussi pour solutioner equations en difference(finite) similaire a eq. diff. ord.
pour avance je crois il besoin comment factorise Pol. de Bernulli
-
grandanois
- Membre Naturel
- Messages: 11
- Enregistré le: 03 Sep 2009, 16:13
-
 par grandanois » 15 Sep 2009, 09:39
par grandanois » 15 Sep 2009, 09:39
a nightmare probleme avec
tous g 2. der : integral f*g =0 =>f polinomi de 1. grad
j´fait une g(x) = un integral dobble qui accumule la discrepance=D= (f-ax-b)
avec manipulation on duduce D =0
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 15 Sep 2009, 10:55
par girdav » 15 Sep 2009, 10:55
Il me semble que j'ai oublié de conclure.
En utilisant les deux relations que j'ai écrites hier, on obtient que
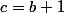^{c-1})
On suppose
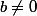
.
On montre que

donc
^{c-1} \geq 2^{c-1} > c)
si

et l'inégalité n'est pas satisfaite.
Pour
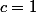
on obtient

ce qui pouvait se déduire avec écriture des sommes.
Pour
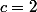
on a
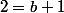^{2-1})
soit
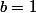
et
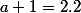
soit
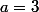
et on récupère le résultat "bien connu".
Pour
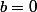
on retrouve le cas
 = \(0,0,1\))
.
Conclusion: les triplets solutions sont
\}\cup\{\(m,m,1\),m\in \mathbb{N}\})
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 15 Sep 2009, 16:21
par Nightmare » 15 Sep 2009, 16:21
Niquel :happy3:
Qu'en penses-tu niveau difficulté pour des sup d'un bon niveau?
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 15 Sep 2009, 17:22
par girdav » 15 Sep 2009, 17:22
Ca doit être faisable: soit ils pensent en terme de polynômes donc du point de vue algébrique, soit ils pensent en terme de sommes de Riemann donc du point de vue analytique, mais dans les deux cas ces notions sont, il me semble dans le programme de sup.
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 15 Sep 2009, 19:18
par Nightmare » 15 Sep 2009, 19:18
Oui oui je ne parlais pas de difficulté en terme d'outils employés mais plutôt en terme de réflexion.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 74 invités
?
