Bonjour,
Je suis entrain d'étudier la méthode de Newton pour l'approximation de zéro d'une fonction numérique réelle.
Je fais la démonstration de la partie du théorème qui donne une majoration de |u_(n+1) - X | où X est le zéro de la fonction f.
Voilà ce qui m'embête :
On considère la fonction f de classe C² sur [a,b], f'>0 et f''>0. Soit X le zéro de la fonction f.
On sait que la fonction définie par Q(t) = t - (f(t)/f'(t)) stabilise l'intervalle [X,b].
Je calcule |u_(n+1) - X| = |(u_n - X)*f'(u_n) - f(u_n)|/|f'(u_n)|.
Dans plusieurs livres je trouve ceci : on utilise la formule de Taylor-Lagrange, donc il existe m dans ]X, u_n[ (puisque seulement [X,b] est stabilisé par Q) tel que :
f(X) = f(u_n) + f'(u_n)*(X - u_n) + f''(m)*(X - u_n)²/2.
Seulement si j'applique la formule sur ]X, u_n[ , je devrais avoir
f(u_n) = f(X) + f'(X)*(u_n - X) + f''(m)*(u_n - X)²/2.
Mais f(X) = 0, et alors cette formule n'est pas valable...
(Et en plus X - u_n < 0)
Je ne vois pas d'où provient mon erreur. Pourriez-vous m'expliquer s'il vous plaît ?
Merci par avance !
Méthode de Newton
4 messages
- Page 1 sur 1
Les deux formules que tu donne:
1) f(X) = f(u_n) + f'(u_n)*(X - u_n) + f''(m)*(X - u_n)²/2.
2) f(u_n) = f(X) + f'(X) *(u_n - X) + f''(m)*(u_n - X)²/2
sont toutes les deux valables (sauf qu'évidement, ce n'est pas forcémént le même m dans les deux) et le fait que f(X)=0 ne pose aucun problème ni dans l'une, ni dans l'autre...
Par contre, vu le résultat de |u_(n+1) - X|=... la première formule est plus utile que la deuxième.
Je pense que ton problème vient du fait que tu ne visualise la formule de taylors que sur [a,b] (avec a
Je pense que la meilleure facon de l'exprimer est :
Pour a et x tels que f soit de classe C^k entre a et a+x (i.e sur [a+x,a] si x<0 ou bien sur [a,a+x] si x>0) on a :
f(a+x)=f(a) + f'(a) x + f''(a)/2! x² + ... + f^(k-1)(a)/(k-1)! x^(k-1)
+f^(k)(a+y)/k! x^k
où y est entre 0 et x (i.e. dans [x,0] ou dans [0,x])
Dans cette formulation, il est bien plus explicite que le x peut bien sûr être positif mais il peut aussi être négatif...
Comme la preuve de ce théorème utilise le Théorème des Accroissements Finis, il suffit de voir que l'égalité f'(c)=(f(b)-f(a))/(b-a) peut s'écrire
1) f(b)=f(a)+f'(c)(b-a)
ou bien 2) f(a)=f(b)+f'(c)(a-b)
(ici, les deux formules disent exactement la même chose, mais, dans la formule de taylors à l'ordre k>=2, dans la formule 1) il apparait des f'(a), f''(a)... alors que dans la 2), c'est des f'(b), f''(b)... et les deux ne disent plus la même chose)
1) f(X) = f(u_n) + f'(u_n)*(X - u_n) + f''(m)*(X - u_n)²/2.
2) f(u_n) = f(X) + f'(X) *(u_n - X) + f''(m)*(u_n - X)²/2
sont toutes les deux valables (sauf qu'évidement, ce n'est pas forcémént le même m dans les deux) et le fait que f(X)=0 ne pose aucun problème ni dans l'une, ni dans l'autre...
Par contre, vu le résultat de |u_(n+1) - X|=... la première formule est plus utile que la deuxième.
Je pense que ton problème vient du fait que tu ne visualise la formule de taylors que sur [a,b] (avec a
Je pense que la meilleure facon de l'exprimer est :
Pour a et x tels que f soit de classe C^k entre a et a+x (i.e sur [a+x,a] si x<0 ou bien sur [a,a+x] si x>0) on a :
f(a+x)=f(a) + f'(a) x + f''(a)/2! x² + ... + f^(k-1)(a)/(k-1)! x^(k-1)
+f^(k)(a+y)/k! x^k
où y est entre 0 et x (i.e. dans [x,0] ou dans [0,x])
Dans cette formulation, il est bien plus explicite que le x peut bien sûr être positif mais il peut aussi être négatif...
Comme la preuve de ce théorème utilise le Théorème des Accroissements Finis, il suffit de voir que l'égalité f'(c)=(f(b)-f(a))/(b-a) peut s'écrire
1) f(b)=f(a)+f'(c)(b-a)
ou bien 2) f(a)=f(b)+f'(c)(a-b)
(ici, les deux formules disent exactement la même chose, mais, dans la formule de taylors à l'ordre k>=2, dans la formule 1) il apparait des f'(a), f''(a)... alors que dans la 2), c'est des f'(b), f''(b)... et les deux ne disent plus la même chose)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Bonjour à tous, j'ai un exercice noté à rendre et je n'arrive pas du tout à le faire si quelqu'un peut me donner un peu d'aide ce serait très gentil. C'est en anglais :
1. Use the Newton-Raphson method to fi nd to an accuracy of 5 decimal
places the 3 largest values of x at which the tangents to the curves y = exp(x)
and y = cos(x) are parallel.
En utilisant la méthode de Newton-raphson pour trouver une estimation à 5 décimales, les 3 valeurs de x pour lesquells les tangentes des fonctions y=exp(x) et y=cos(x) sont parallèles.
1. Use the Newton-Raphson method to fi nd to an accuracy of 5 decimal
places the 3 largest values of x at which the tangents to the curves y = exp(x)
and y = cos(x) are parallel.
En utilisant la méthode de Newton-raphson pour trouver une estimation à 5 décimales, les 3 valeurs de x pour lesquells les tangentes des fonctions y=exp(x) et y=cos(x) sont parallèles.
bonjour,
c'est bizarroïde, l'équation
=0) semble avoir une infinité de solutions dans
semble avoir une infinité de solutions dans 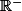
ah oui, ils demandent les trois plus grandes solutions !!!
l'équation n'a pas de solution strictement positive car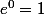
si x>0)
ça suggère d'appliquer la méthode de Newton en partant de
 ?
?
une fois encadrée la 1ère racine
il faut trouver une nouvelle initialisation à gauche de ??
??
mais les courbes représentatives de
exp()+sin()
et de
sin()
sont asymptotes l'une de l'autre quand x tend vers
Leurs zéros sont à peu de choses près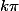
c'est bizarroïde, l'équation
ah oui, ils demandent les trois plus grandes solutions !!!
l'équation n'a pas de solution strictement positive car
si x>0
ça suggère d'appliquer la méthode de Newton en partant de
une fois encadrée la 1ère racine
il faut trouver une nouvelle initialisation à gauche de
mais les courbes représentatives de
exp()+sin()
et de
sin()
sont asymptotes l'une de l'autre quand x tend vers
Leurs zéros sont à peu de choses près
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 54 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
