Exercice Syteme 3 inconnus DM

[MG9]

SaLut ! je bloque a mon exercice de maths ou je dois trouver 3 nombres; voila l'énonce :
Cherchez 3 nombres tel que: le 1er augmenté de 73 égale le double de la somme des 2 autre, le 2nd augmenté de 73 egale le triple de la somme des 2 autres, le 3e augmenté de 73 égale le quadruple de la somme des 2 autres.

Voila ce que j'ai fait : x= 1er nb
y= 2e nb
z= 3e nb

{2y+2z=x+73
{3x+3z=y+73
{4y+4x=z+73

J'ai 2 questions : est-ce que mon systeme est bon et comment finir cet exo ?
:help:
merci !

[Dinozzo13]

Je dirai que c'est bon, je réécris ton système pour mieux le résoudre ^^ :

[Dinozzo13]

Si tu connais, tu peux utiliser la méthode du pivot de Gauss qui consiste à choisir une des équations, la plus facile en générale, pour supprimer un des termes commun aux deux autres équations de ce système. Veux-tu que je t'aide à procéder ainsi ?

[MG9]

Ué je veux bien !
je peux enlever les "y" non ?

[benekire2]

Commence par soustraire la une et la trois^^ .

[MG9]

c'est pour enlever les "x" non ? :

-x+2y+2z=73
2x+2y-z=73

Je multiplie par 2 la 1ere ligne :

-2x-4y-4z= -146
2x+2y-z = 73
----------------------
2y-3z = -73


c'est "-3z" ou "-5z" ?

[Dinozzo13]

Alors attention, 'faut bien suivre ^^, c'esst un peu lourd à dire à l'écrit ^^.
Pour commencer nommons les 3 équations.

On va choisir l'équation comme équation "pivot", c'est-à-dire qu'elle va nous servir, en la manipulant, à éliminer les termes en des deux autres équations. Une fois cela fait, on résoudra et comme système de deux équations à deux inconnues, on trouvera et , il ne restera plus qu'à en déduire .
Pour cela, on doit modifier notre système de trois équations à trois inconnues ; Comme est notre équation pivot, on y touche pas, elle nous servira à en déduire :

On remarque qu'il y a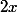 à la deuxième et troisième équation, et, qu'il y a un terme différent (ici ) à l'équation pivot, il faut donc trouver un facteur tels que l'on puisse supprimer ces termes en de la deuxième et troisième équation c'est-à-dire trouver un nombre entier tel que , ici, je te l'ai mis pour t'orienter, c'est , à toi de le faire le reste ^^.

[MG9]

c'est ce que jai fait a la reponse precedente de la tienne nan ?

-x+2y+2z=73
2x+2y-z=73

Je multiplie par 2 la 1ere ligne :

-2x-4y-4z= -146
2x+2y-z = 73
----------------------
2y-3z = -73


c'est "-3z" ou "-5z" ?

[Dinozzo13]

bah ché pas, si je met en ligne ^^, réfléchis bien :

[MG9]

jdirais -5z...

Après je fais la meme chose pour (E) et (E2) mais cette fois pour " z" ?

[Dinozzo13]

nam, lis bien ce que j'ai mis, tu fait pareil avec les "x" de . Et d'ailleurs c'est -2y pas 2y ^^

[MG9]

Jcomprends pas là


-2x-4y-4z= -146
2x+2y-z = 73
----------------------
-2y-5z = -73

ce que j'ai fait avant c'est entre (E) et (E2) pour les 'x'

et là je peut le faire pour (E1) :

-x+2y+2z=73
2x-y+2z=73

je multiplie la 1ere ligne par 2

-2x-4y-4z = -146
2x-y+2z = 73
-------------------
-5y - 2z = 73


Pui j'ai un systemede 2 equations :

{-2y-5z = -73
{-5y - 2z = 73

je multiplie par -5 la 1ere ligne et par 2 pour la 2e ligne pour que je puisse enlever les 'y'

10y + 25 z = 365
-10y - 4z = 146
-----------------------
21z = 511
z = 511 / 21 = 73/3

donc z= 73/3

aprés je remplace z de l'équation -2y-5z = -73 par 73/3 ou je fais lameme chose pour 'y'?

[Dinozzo13]

Pui j'ai un systemede 2 equations :

{-2y-5z = -73
{-5y - 2z = 73
(...)
aprés je remplace z de l'équation -2y-5z = -73 par 73/3 ou je fais lameme chose pour 'y'?

Bah, si t'a z, tu peux le remplacer pour trouver y, oui.

[MG9]

-2y-5(73/3)= -73
-2y = -365/3 +73
2y = 365/3 -219/3
2y = 146/3
y = 73/3

[MG9]

ensuite pour x :
-x+2(73/3)+2(73/3) = 73
x = 146/3+146/3-73
x = 292/3 -73
je multiplie 73 par 3
x = 292/3 - 219/3
x = 73/3



donc S{73/3;73/3;73/3}

Est-ce que j'ai bon ? :id: :id: :id:

[benekire2]

Le pivot de gauss sur le plan matriciel c'est marrant http://fr.wikipedia.org/wiki/%C3%89limination_de_Gauss-Jordan

[MG9]

C'est bon ? ou pas ?

[MG9]

Tu t'est tromper dans ton systeme ce qui a tout faussé voila la solution j'ai verifié et c'est bon :zen:

voila mes calculs :

Page 1

Page 2

[Timothé Lefebvre]

Le pivot de gauss sur le plan matriciel c'est marrant [url="http://fr.wikipedia.org/wiki/%C3%89limination_de_Gauss-Jordan"]http://fr.wikipedia.org/wiki/%C3%89limination_de_Gauss-Jordan[/url]

Tiens je suis en train de rédiger un cours là-dessus, comme pour les sommes-produits

@ MG9 : toi tu te fous royalement du monde : http://www.ilemaths.net/forum-sujet-309811.html

[MG9]

ba jvoulais avoir plusieurs avis