Sytème d'équation

[Safran01]

Bonjour,

J'ai un devoir à faire et je suis coincée sur un exercice, si vous pouvez me mettre sur la voie, merci !

a+b=1
a^2+b^2=3

C'est un système de 2 équations.

La question :
que vaut ab ? Démontrer que a^4+b^4 est un entier.

Merci
Safran01

[mcar0nd]

Bonjour,

J'ai un devoir à faire et je suis coincée sur un exercice, si vous pouvez me mettre sur la voie, merci !

a+b=1
a^2+b^2=3

C'est un système de 2 équations.

La question :
que vaut ab ? Démontrer que a^4+b^4 est un entier.

Merci
Safran01

Salut, à partir de la première équation, tu peux écrire que , et ensuite injecter ça dans la deuxième équation afin de n'avoir plus qu'une seule inconnue.

[Safran01]

Ok, merci je trouve que b = 1 du coup a=0 ?
donc ab = 0 et a^4+b^4 = 0^4 + 1^4 = 1 qui est bien un entier

[mcar0nd]

Ok, merci je trouve que b = 1 du coup a=0 ?
donc ab = 0 et a^4+b^4 = 0^4 + 1^4 = 1 qui est bien un entier

Est ce que tu pourrais mettre tes calculs s'il te plaît, parce que tu t'es trompé, tes solutions pour a et b ne sont pas bonnes.

[Safran01]

Oui, je m'en suis aperçue juste après avoir posté.
donc :
(1-b^2)+b^2=3
1-2b+b^2+b^2=3
1-2b+2b^2=3
-2b^2=3-1+2b
-2b^2=2+2b
b^2=2+2b/2
b=V2+2b/2

Voilà,....

[mcar0nd]

Oui, je m'en suis aperçue juste après avoir posté.
donc :
(1-b^2)+b^2=3
1-2b+b^2+b^2=3
1-2b+2b^2=3
-2b^2=3-1+2b
-2b^2=2+2b
b^2=2+2b/2
b=V2+2b/2

Voilà,....

Tu as mis des moins en trop et tu les as oubliés à la fin.
Donc, on reprend, ta deuxième équation c'est , que tu sais résoudre avec le discriminant et le calcul des racines.

[Safran01]

donc la suite :
2b^2=2b+2
b^2=2b+2/2
b=V2b

ça me semble encore faux j'arrive pas à éliminer b...

[mcar0nd]

donc la suite :
2b^2=2b+2
b^2=2b+2/2
b=V2b

ça me semble encore faux j'arrive pas à éliminer b...

Pour résoudre , tu utilises le discriminant . Tu connais?

[Safran01]

Non, ça fait longtemps que j'ai quitté l'école...dur dur de s'y remettre ! merci pour ta patience et tes réponses rapides

[mcar0nd]

Non, ça fait longtemps que j'ai quitté l'école...dur dur de s'y remettre ! merci pour ta patience et tes réponses rapides

Bah en calculant le discriminant, tu trouves
D'où ensuite tu as les deux solutions et .
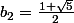
Ensuite tu injecte ça dans la première équation de départ et tu trouve a.

[Safran01]

ok, c'est bien compliqué pour moi tout ça...merci ! bien

[mcar0nd]

ok, c'est bien compliqué pour moi tout ça...merci ! bien

Tu injectes ses solutions dans la première équation et ensuite tu peux facilement trouver a.