J'ai un DM à rendre pour Mardi, mais il y a un exercice que j'ai du mal à comprendre, voici l'énoncé :
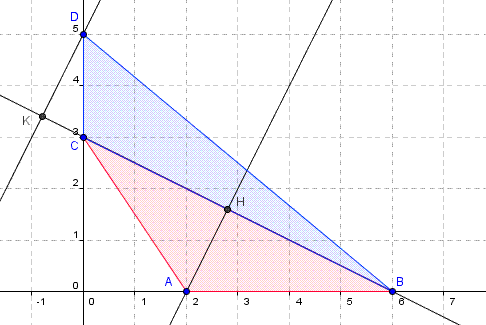
Dans un repère orthonormal A(2;0), B(6;0) , C(0;3) et D(0;5)
Par A et D on trace les perpendiculaires à la droite (BC)
elles coupent (BC) respectivement en H et K
a) évaluer de deux manières différentes l'aire du triangle ABC
puis l'aire du triangle BCD
b) en déduire que A et D sont équidistants de la droite (BC)
a) J'ai calculé AB et BC,
Aire ABC = AB * CO/2
= 4 * 3/2
= 6
Aire ABC = OB * OC / 2 - OA * OC /2
= (6 * 3 / 2) - (2 * 3 /2)
= 9 - 3
= 6
Donc l'aire du triangle ABC est de 6cm²
-----
Je calcule BD
Aire BCD = BO * CB / 2
= 6 * 2 / 2
6
Aire BCD = Aire OBD - Aire OBC
= Je passe les calcule, j'ai aussi trouvé 6 cm²
b) C'est là que ça me pose problème, on doit prouvé que A et D sont équidistant à la droite BC donc AH = DK,
Or l'énoncé dit "En déduire" donc ça veut dire que la solution découle du a) mais comme K ne fais pas parti de BCD je vois pas comment on peut arrivé à la solution en partant du a), surtout que le prof a dit qu'on a pas besoin de calculer AH et DK
Pouvez vous m'aider s'il vous plait ? J'arrive pas à comprendre la démarche, ne me donnez pas la solution, mais juste un petit coup de pouce svp.
Merci :we:
