Un point fixe est un attracteur

[Anonyme]

Bonsoir tous.
je suis en deuxieme année de prépa. Mon TIPE porte sur le chaos (je sais, c'est super original, m'enfin, bon!) et je voudrais savoir comment démontrer qu'un point fixe x0 d'une fonction f (parabole) est un attracteur de f. je veux montrer que |f'(x0)| < 1 => x0 point fixe attracteur. j'ai un magazine qui explique la démonstration, mais je la trouve un peu olé olé !! "on fait comme si le triangle ..." etc.. je trouve ca moyen meme si je ne suis pas contre une demonstration géometrique. (d'ailleurs, je viens d'essayer de dessiner ce fameux triangle... ben mes cotés, ils se ne rejoignent pas où il faut...!!) ..
merci d'avance

[Proutiste]

Bonjour, moi c'est Pingouin le copain, je suis en deuxième année de Bio et là...WOUAAAAA, je me dit:
"tiens si je polluais un peu ce forum où ils se posent des questions si existentielles qu'ils vont en oublier de s'occuper de l'environnement^^
enfin, non rien à voir
Juste une envie assumée et totalement stupide, de venir polluer ce post!
Voilà!
je vous remercie!
Et pour comprendre le chaos...ben bon courage^^
Aussi évident que le Chat de Schrodinger, (oui plus dur que celui de Gelluk, quoi que des fois celui là...)

EDIT: oui en effet "membre naturel^^ Sans aucun OGM qui ne sont pas spécialement dangereux non plus, que ce soit dit :)

[Anonyme]

adrien t'es un idiot... il n'empeche, ma question etait tres serieuse...

[abcd22]

Bonjour !
On commence par montrer qu'il existe tels que (ça vient de la continuité de f').
Ensuite, on montre grâce au théorème des accroissements finis que est stable par f.
Puis on montre que si on choisit dans ce segment et qu'on définit une suite par 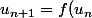, pour tout n, (par récurrence, encore avec les accroissements finis), ce qui montre que la suite converge vers .
C'est pas au programme en prépa ça au fait ?

[Anonyme]

c'est vrai que dans le cours sur les suites, on a enoncé cette propriété, mais "hors-programme" ... arf.. c'est juste histoire de savoir à vu de nez si ca converge ... en tout cas merci beaucoup !