Arcsin Complexe
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
 par benoit.roubert » 21 Sep 2009, 14:53
par benoit.roubert » 21 Sep 2009, 14:53
Bonjour,
Quelqu'un pourrait-il m'expliquer comment la fonction ArcSin est définie pour un nombre complexe ?
Mon problème réside notemment en la résolution d' équations du type :
) = k >1)
et à trouver le z correspondant.
En remerciant d'avance tous ceux qui pourront m'éclairer
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
 par Pythales » 21 Sep 2009, 16:13
par Pythales » 21 Sep 2009, 16:13
Par analogie avec le domaine réel

donne

et en posant

on obtient

soit

et

, le radical étant pris avec une détermination particulière.
On en tire

, ce qui ramène la fonction à un logarithme.
 par benoit.roubert » 22 Sep 2009, 13:06
par benoit.roubert » 22 Sep 2009, 13:06
Merci de votre réponse,
Néanmoins je reste un peu bloqué avec cette expliquation car cela me donne l'impression d'avoir
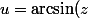 \Leftrightarrow z = \sin(u) = \frac{e^{2 i u}-e^{-2 i u}}{2i})
et du coup par exemple :
 = \frac{\pi}{2} \Rightarrow z=\sin(\frac{\pi}{2}) = 1)
 = \frac{3\pi}{2} \Rightarrow z=\sin(\frac{3\pi}{2}) = 1)
et du coup on a la même valeur de z pour des arcsin(z) différents.
Je dois m'embrouiller quelquepart
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
 par Pythales » 22 Sep 2009, 14:24
par Pythales » 22 Sep 2009, 14:24
Si
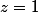
,
=\frac 1i\ln(i)=\frac 1i\ln e^{i\frac{\pi}2}=\frac{\pi}2)
Si
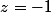
,
=\frac 1i\ln(-i)=\frac 1i\ln e^{-i\frac{\pi}2}=-\frac{\pi}2)
le log étant défini à

près
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 45 invités