Inéquations avec ln et exp

[Skuld]

Hum, alors voilà je dois résoudre cette inéquation :
2 ln(1-x) < 1

J'ai commencé par chercher le domaine de validité, et je trouve Dval = ] 0;1 [

Puis,

2 ln ( 1-x ) < 1
ln (( 1-x)²) < 1
exp (ln ((1-x)²)) < exp(1)
( 1 - x )² < e

C'est ici que je suis bloquée.
J'ai essayé de developper et je trouve :

1 - 2x + x² < e
-2x + x² < e - 1
x ( - 2 + x ) < e- 1

Seulement ça ne m'a pas vraiment avancée =D
Merci de votre aide.

[fatal_error]

salut,

plusieurs possibilités :


tu peux faire apparaitre
en posant
Tu peux aussi factoriser a coups de trinomes :

[Skuld]

Merci =D

Cependant, je trouve ensuite que Delta = 4e (?)

Et pour la recherche de x1 et x2 la racince carré de (4e) me bloque =O

[fatal_error]

re,

ben laisse alors (ou mieux : )

[Ericovitchi]

Et plus simplement

[Skuld]

Euh. Je ne comprend pas comment tu arrives à ça.
Après avoir fait x1 et x2, j'ai fait un tableau de signes.
Et au final je trouve S = ] 0 ; 2 - [

Mais je suis pas sure de moi du tout en fin d'compte =O

[Ericovitchi]

tu as raison il faut tenir compte du domaine de définition donc prendre zéro comme borne de gauche. Par contre à droite je ne vois pas bien comment tu trouves ça.

Sinon en relisant tes calculs du début tu as fait bien compliqué car quand tu en es à 2 ln ( 1-x ) < 1 , au lieu de fabriquer un carré qui t'a amené plein d'ennuis, il était plus simple de faire donc et donc le

[Skuld]

En fait comme je l'ai dit plus haut, après en être arrivé à x² - 2x + ( 1- e) < 0
J'ai calculé delta, j'ai trouvé = 4e
x1= 2 -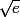
x2= 2 +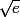

A partir de là je ne sais pas si c'est bon car après avoir trouvé ça j'ai fait un tableau de signes. Et ma borne de droite viens de là.


Je viens d'essayer sans mon carré du début, et au final je trouve x < - (e 1/2) -1
Ca fait environ - 2.35 non ? Mais ca ne rentre pas dans le domaine de validité alors ? En réalité il n'y a pas de solution si ?

[fatal_error]

re,

ca serait cool si tu pouvais ecrire les etapes de calcul. Parce que les resultats parachutés, si jamais ils sont faux...sait-on jamais :we:

[Skuld]

Il n'y a pas d'étapes de calcul pour le coup, si c'est à moi que tu parles =D

J'ai suivis ce que disais Ericovitchi, et ca m'a donné ça.

Mon -2.35 est approximatif, "e" est environ égal à 2.7 si je ne me trompe pas =O donc -e( 1/2) - 1 = à peu près -2.35.

Il faudrait donc que x < - 2.35 , or avec le domaine de validité il ne peut pas être inferieur à 0. J'en ai donc conclut qu'il n'y avait pas de solution, mais je ne suis absolument pas certaine de mes déductions =D

[Ericovitchi]

Tu t'entêtes à trouver des racines fausses.

x² - 2x + ( 1- e) =0

[Skuld]

Ah oui pardon.

Dans ce cas là, puisque les + sont à l'exterieur des racines, je trouve finalement que les solutions sont S = ] 0 ; 1 [