Dm Vecteurs Seconde.

par **Mllexchonchon** » 15 Avr 2009, 13:08

Bonjour, je bloque sur un exercice sur les vecteurs. Voici l'énoncé :

Soit les points A(-3;-2), B(1;4) et C(5;3)
Calculer les coordonnées du point D de sorte que le quadrilatère ABCD soit un trapèze de bases [AB] et [CD] dans le cas où D est un point de :
[CENTER]a. L'axe des abscisses
b. L'axe des ordonnées
c. La droite d'équation y= 2x-3[/CENTER]

Je suis vraiment perdue et j'ai beau cherché dans mes cours, mon livre ou sur internet je ne te trouve aucune information pouvant m'aider à commencer le problème.

Merci d'avance d'essayer de me mettre sur la bonne voie

par **uztop** » 15 Avr 2009, 13:17

Bonjour,

pour le cas a. par exemple, tu veux que D soit sur l'axe des abscisses, c'est a dire que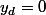

.
Tu veux aussi que ABCD soit un trapeze de bases [AB] et [CD], cela signifie que (AB) // (CD). Avec ca tu as assez de renseignements pour trouver

Pour le b le principe est le meme sauf que c'est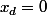

Pour le c, il faudra resoudre un petit systeme d'equations.

par **Mllexchonchon** » 15 Avr 2009, 14:06

Les coordonnées du point D seraient donc (xa;ya) ?

Je ne comprends pas la méthode :S

Pour le a. (AB) et (CD) devrait donc avoir le même coefficient directeur ?

par **mariie64** » 15 Avr 2009, 14:17

uztop a écrit:Bonjour,

pour le cas a. par exemple, tu veux que D soit sur l'axe des abscisses, c'est a dire que .
Tu veux aussi que ABCD soit un trapeze de bases [AB] et [CD], cela signifie que (AB) // (CD). Avec ca tu as assez de renseignements pour trouver

Pour le b le principe est le meme sauf que c'est

Pour le c, il faudra resoudre un petit systeme d'equations.

on szn fout de ta vieeeeeeeeee !!! ta geule

par **mariie64** » 15 Avr 2009, 14:19

ta geuleeeeeeeeeee

par **uztop** » 15 Avr 2009, 14:20

mariie64 a écrit:on szn fout de ta vieeeeeeeeee !!! ta geule

?? pourquoi tu dis ca ??

Pour Mllexchonchon, oui (AB) et (CD) doivent avoir le meme coefficient directeur, je repasserai plus tard quand j'aurai plus de temps

par **oscar** » 15 Avr 2009, 14:43

Bonjour: Je peux me permettre de donner mon avis scp

A( -3;-2); B ( 1;4) C( 5;3)
Soit D (x; y)

ABCD trapèze si (AB)//(CD)
Coord de AB ( 4; 6) de CD( x-5; y-3)
VAB et V CD colinéaires si 4*(y-3) = 6*(x-5) ( uv" = u'v)
ON a ainsi 4y-12=6x-30 ou y= 3/2 x + 9/2 (1)

On peut alors considérer les 3 cas

Soit D point de Oy ou x=0 on cherche ensuite y
Soit D point de OX ou y = 0; on cherche ensuite x
Soit (CD) a pour éqution y = 2x--3: on compare avec (1)

Voila le résultat de ma recherche ???Qu' en pense notre Modérateur?

par **Mllexchonchon** » 15 Avr 2009, 16:36

oscar a écrit:ON a ainsi 4y-12=6x-30 ou y= 3/2 x + 9/2 (1)

Le résultat n'est pas plutôt y = 3/2x - 9/2
Car 12-30 = -18 !

Je n'arrive pas à trouver le petit a quand y doit être = 0
Je n'ai pas encore cherché le c

par **oscar** » 15 Avr 2009, 16:50

D' accord pour le - 9/2
Donc y = 3/2x - 9/2(1)

a) y=0, car D sur l' axe Oy tu remplaces dans (1) => 0= 3/2x -9/2=> x=3
b) x=0, y=
c) Je te laisse encore chercher

par **Mllexchonchon** » 15 Avr 2009, 17:13

Super :D
Alors en ce qui concerne ce que j'ai trouvé :

b. Y= -9/2 soit -4.5
c. Y= 3/2x - 9/2 et Y' = 2x - 3
3/2x - 9/2 = 2x - 3
3/2x - 2x = -3 + 9/2
-1/2x = 3/2
x = -3

On remplace x dans une des deux équations :
y = 2x - 3
y = (2*-3) -3
y = -9

J'ai vérifié en faisant une figure et mes résultats parraissent plausibles.

Ils le sont ? :$

par **oscar** » 15 Avr 2009, 21:48

C' est très bien
Tu te débrouilles vite et bien

par **Mllexchonchon** » 16 Avr 2009, 08:41

Merci beaucoup à toi et uztop.
C'est très gentil :]

Dm Vecteurs Seconde.

Dm Vecteurs Seconde.

dm de math

Qui est en ligne