Bonjour à tous !
Voila, je suis en école d'ingénieur et aujourd'hui nous avions à trouver les coordonnées d'un point en fonction de 3 distances et de 3 points. Je vais vous énoncer l'exercice plus bas. Je n'arrive pas à tomber sur le même résultat que le prof.
Donc pour l'exercice :
"Soient les points A(600, 100), B(600, 800) et C(300, 300). Soient les distances AM=100\/¯27 BM=100\/¯10 et CM=200\/¯2. Trouvez M".
Après un changement de repère, nous avons mis A en origine du nouveau repère, ce qui donnent les nouvelles coordonnées : A(0,0), B(0, 700), C(-300, 200) et M(X-600, Y-100).
Après résolution d'équations, nous avons trouvé que pour trouvé l'ordonnée de M, la formule à utiliser était la suivante :
Ym = (Da² - Db²+Yb)/2Yb (avec Da = AM et Db = BM)
Le résultat trouvé en cours est de 400 hors changement de repère.
Je n'arrive pas à ce résultat, je trouve desespérement 50,5.
Si quelqu'un pouvait m'éclairer... merci d'avance !
Calcul de coordonnées de points
8 messages
- Page 1 sur 1
par mathelot » 01 Avr 2009, 09:32
Bj,
repère orthonormé de base)
On choisit ensuite le repère affine (A,B,C), d'origine A, de vecteurs de base
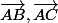
Le fait de connaitre la distance AM et la formule d'Al-Kashi
donnant les cosinus des 3 angles d'un triangle, incite
à travailler momentanément en coordonnées polaires:
=cos(\vec{AB},\vec{AM})=\frac{AM^2+AB^2-BM^2}{2 AM.AB})
En coordonnées polaires, on travaille implicitement
avec une base orthonormée directe
.
Données numériques:
tous est multiple de 100, nous ne tenons pas compte de ce facteur:
=\frac{27+49-10}{42\sqrt{3}}=\frac{11}{7\sqrt{3}})
° ou 
°
|=\sqrt{1-cos^2(\theta)}=\frac{\sqrt{26}}{7\sqrt{3}})
avec le déterminant,
=21 > 0)
donc le triangle ABC est direct.
solution bovine:
Le problème, c'est que ça donne deux solutions pour l'angle polaire
. on calcule les coordonnées cartésiennes correspondantes
et on élimine la solution qui ne convient pas.
içi>0)
repère orthonormé de base
On choisit ensuite le repère affine (A,B,C), d'origine A, de vecteurs de base
Le fait de connaitre la distance AM et la formule d'Al-Kashi
donnant les cosinus des 3 angles d'un triangle, incite
à travailler momentanément en coordonnées polaires:
En coordonnées polaires, on travaille implicitement
avec une base orthonormée directe
Données numériques:
tous est multiple de 100, nous ne tenons pas compte de ce facteur:
avec le déterminant,
solution bovine:
Le problème, c'est que ça donne deux solutions pour l'angle polaire
et on élimine la solution qui ne convient pas.
içi
résolution graphique sur une feuille de brouillon!
par mathelot » 02 Avr 2009, 09:19
Bj,
On divise toutes les coordonnées et distances par 100,
on se place en :
il vient
A(6,1);B(6;8),C(3;3).
Le point M à l'intersection des trois cercles a graphiquement pour coordonnées
(3,8;5,7), soit en tenant compte de la réduction d'un facteur 100:
M(380;570)
On divise toutes les coordonnées et distances par 100,
on se place en :
il vient
A(6,1);B(6;8),C(3;3).
Le point M à l'intersection des trois cercles a graphiquement pour coordonnées
(3,8;5,7), soit en tenant compte de la réduction d'un facteur 100:
M(380;570)
Calcul exact des coordonnées de M (inquiétant, je trouve pas
par mathelot » 02 Avr 2009, 09:49
re,
On passe en coordonnées polaires.
repère polaire, d'origine A. On norme le vecteur
,
ce qui donne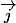
. la base orthonormée directe
est donc)
M a pour coordonnées polaires, dans le repère polaire)
=\frac{11}{7\sqrt{3}})
M a pour coordonnées cartésiennes dans le repère polaire
:
)
d'où
}{7} \vec{i} + \frac{40}{7} \vec{j})
en multipliant par 100, les coordonnées exactes de M sont:
}{7} ; \frac{4000}{7} \right) \sim (381;571))
remarque: en essayant de déterminer si l'ordonnée de M
est positive dans le repère non orthogonal)
, on s'aperçoit que le signe des produits scalaires
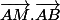et 
ne donne pas la réponse sur le signe de)
, car justement le repère (A,B,C) n'est pas orthogonal.
Comme intersection de trois cercles, le point M est connu
par ses trois projetés orthogonaux)
sur les droites (AB),(AC),(BC).
à suivre....
On passe en coordonnées polaires.
repère polaire, d'origine A. On norme le vecteur
ce qui donne
est donc
M a pour coordonnées polaires, dans le repère polaire
M a pour coordonnées cartésiennes dans le repère polaire
d'où
en multipliant par 100, les coordonnées exactes de M sont:
remarque: en essayant de déterminer si l'ordonnée de M
est positive dans le repère non orthogonal
ne donne pas la réponse sur le signe de
Comme intersection de trois cercles, le point M est connu
par ses trois projetés orthogonaux
sur les droites (AB),(AC),(BC).
à suivre....
par Black Jack » 02 Avr 2009, 11:19
Ou pourquoi faire simple quand on peut faire compliqué.
Sans changement de repère.
AM² = (600-X)²+(100-Y)² = 27.10^4 (1)
BM² = (600-X)²+(800-Y)² = 10^5 (2)
CM² = (300-X)²+(300-Y)² = 8.10^4 (3)
(2)-(1) --> (800-Y)² - (100-Y)² = 10^5 - 27.10^4
800² - 1600Y + Y² - (10000-200Y+Y²) = -1,7.10^5
1400Y = 800000
Y = 571,428571429
Dans (2) -->(600-X)²+(800-571,428571429)² = 10^5
(600-X)² = 47755
X = 600 +/- V47755
X = 381,47 ou X = 818,53
Il faut vérifier dans (3) :
a)
X = 818,53 et 571,428571429
(300-818,53)² + (300-571,428571429)² = 342567--> ne convient pas.
b)
X = 381,47 et 571,428571429
(300-381,47)²+(300-571,428571429)² = 8,03.10^4 --> OK à un poil près.
M(381,47 ; 571,43)
:zen:
Sans changement de repère.
AM² = (600-X)²+(100-Y)² = 27.10^4 (1)
BM² = (600-X)²+(800-Y)² = 10^5 (2)
CM² = (300-X)²+(300-Y)² = 8.10^4 (3)
(2)-(1) --> (800-Y)² - (100-Y)² = 10^5 - 27.10^4
800² - 1600Y + Y² - (10000-200Y+Y²) = -1,7.10^5
1400Y = 800000
Y = 571,428571429
Dans (2) -->(600-X)²+(800-571,428571429)² = 10^5
(600-X)² = 47755
X = 600 +/- V47755
X = 381,47 ou X = 818,53
Il faut vérifier dans (3) :
a)
X = 818,53 et 571,428571429
(300-818,53)² + (300-571,428571429)² = 342567--> ne convient pas.
b)
X = 381,47 et 571,428571429
(300-381,47)²+(300-571,428571429)² = 8,03.10^4 --> OK à un poil près.
M(381,47 ; 571,43)
:zen:
par mathelot » 02 Avr 2009, 12:55
ou pourquoi faire beau quand on peut faire laid ?
Black Jack,
j'y vais de ma petite critique:
1)
dans cet exemple particulier (AB vertical) on a immédiatement
l'ordonnée de M:
avc le projeté de M sur la droite (AB).
il y avait donc une solution encore plus rapide que la tienne !
2)
les valeurs exactes ne sont pas fournies
3)
le problème , à savoir qu'il faut rejeter une des deux solutions (c'est le même souçi en coord. polaires) n'est pas vraiment résolu
4)
ce qui serait "beau", c'est évidemment d'obtenir les coordonnées de M
dans le cas général, avec une formule symétrique en A,B,C
Black Jack,
j'y vais de ma petite critique:
1)
dans cet exemple particulier (AB vertical) on a immédiatement
l'ordonnée de M:
avc le projeté de M sur la droite (AB).
il y avait donc une solution encore plus rapide que la tienne !
2)
les valeurs exactes ne sont pas fournies
3)
le problème , à savoir qu'il faut rejeter une des deux solutions (c'est le même souçi en coord. polaires) n'est pas vraiment résolu
4)
ce qui serait "beau", c'est évidemment d'obtenir les coordonnées de M
dans le cas général, avec une formule symétrique en A,B,C
par Black Jack » 02 Avr 2009, 15:54
Salut Mathelot
Rien ne précise qu'on désire des valeurs exactes pour X et Y, ni d'ailleurs qu'on ne se contente pas de distances approximatives (à un poil près, poil à définir).
C'est ce qui différentie des calculs d'ingénieurs et de mathématiciens...
Et comme Ellanoise est dans une école d'ingénieurs ...
Par la méthode que j'ai préconisée, on peut trouver les valeurs exactes si elles existent qui satisfont les 3 équations.
En fait, elle n'existent pas et donc du point de vue d'un mathématicien, il n'y a pas de solutions au problème posé...
Mais ce n'est pas vrai du point de vue ingénieur comme je l'ai dit (car cela marche à "un rien" près.)
Voila ci-dessous (aux erreurs de calculs) près la démo, qu'il n'y a pas de solutions mathématiques par la méthode que j'ai employée (mais en gardant les valeurs exactes).
Si on veut pousser les calculs avec les valeurs exactes, on peut aisément le faire puisque les équations (1) et (2) donnent:
Y = 800000/1400 = 4000/7 exactement
et la valeur de X susceptible de convenir est celle issue de :
(600-X)²+(800- 4000/7)² = 10^5
(600-X)² = 2340000/49
X = 600 +/- (300/7)V26
On vérifie donc l'équation (3) avec la valeur exacte de Y issue de(1) et (2), quelles valeurs de X satisfont l'équation (3) et on la compare in fine à celles issues des équations (1) et (2).
(300-X)²+(300- 4000/7)² = 8.10^4
(300-X)² = 310000/49
X = 300 +/- (100/7)*V31
Lex valeurs les plus proches l'une de l'autre de X sont:
Celle issue de (1) et (2) : X = 600 - (300/7)V26
Celle issue de (3) : X = 300 + (100/7)*V31
Ces valeurs sont différentes et donc pas de solutions mathématiques.
Mais X = 600 - (300/7)V26 = 381,47
et X = 300 + (100/7)*V31 = 379,54
Il reste, dans le cadre du problème concret (qu'on ne peut pas deviner à partir de l'énoncé) à décider pour l'ingénieur si ces valeurs de X sont suffisamment proches pour s'en contenter.
Il faut aussi vérifier mes calculs car j'ai tendance à être distrait.
Si je n'ai pas fait d'erreurs, il est clair que chercher les coordonnées exactes de M est impossible, puisque les 3 cercles de centre A, B et C et de rayons adéquats (ceux imposés par l'énoncé) ne sont pas EXACTEMENT concourants.
:zen:
Rien ne précise qu'on désire des valeurs exactes pour X et Y, ni d'ailleurs qu'on ne se contente pas de distances approximatives (à un poil près, poil à définir).
C'est ce qui différentie des calculs d'ingénieurs et de mathématiciens...
Et comme Ellanoise est dans une école d'ingénieurs ...
Par la méthode que j'ai préconisée, on peut trouver les valeurs exactes si elles existent qui satisfont les 3 équations.
En fait, elle n'existent pas et donc du point de vue d'un mathématicien, il n'y a pas de solutions au problème posé...
Mais ce n'est pas vrai du point de vue ingénieur comme je l'ai dit (car cela marche à "un rien" près.)
Voila ci-dessous (aux erreurs de calculs) près la démo, qu'il n'y a pas de solutions mathématiques par la méthode que j'ai employée (mais en gardant les valeurs exactes).
Si on veut pousser les calculs avec les valeurs exactes, on peut aisément le faire puisque les équations (1) et (2) donnent:
Y = 800000/1400 = 4000/7 exactement
et la valeur de X susceptible de convenir est celle issue de :
(600-X)²+(800- 4000/7)² = 10^5
(600-X)² = 2340000/49
X = 600 +/- (300/7)V26
On vérifie donc l'équation (3) avec la valeur exacte de Y issue de(1) et (2), quelles valeurs de X satisfont l'équation (3) et on la compare in fine à celles issues des équations (1) et (2).
(300-X)²+(300- 4000/7)² = 8.10^4
(300-X)² = 310000/49
X = 300 +/- (100/7)*V31
Lex valeurs les plus proches l'une de l'autre de X sont:
Celle issue de (1) et (2) : X = 600 - (300/7)V26
Celle issue de (3) : X = 300 + (100/7)*V31
Ces valeurs sont différentes et donc pas de solutions mathématiques.
Mais X = 600 - (300/7)V26 = 381,47
et X = 300 + (100/7)*V31 = 379,54
Il reste, dans le cadre du problème concret (qu'on ne peut pas deviner à partir de l'énoncé) à décider pour l'ingénieur si ces valeurs de X sont suffisamment proches pour s'en contenter.
Il faut aussi vérifier mes calculs car j'ai tendance à être distrait.
Si je n'ai pas fait d'erreurs, il est clair que chercher les coordonnées exactes de M est impossible, puisque les 3 cercles de centre A, B et C et de rayons adéquats (ceux imposés par l'énoncé) ne sont pas EXACTEMENT concourants.
:zen:
par mathelot » 02 Avr 2009, 16:34
Black Jack a écrit:Si je n'ai pas fait d'erreurs, il est clair que chercher les coordonnées exactes de M est impossible, puisque les 3 cercles de centre A, B et C et de rayons adéquats (ceux imposés par l'énoncé) ne sont pas EXACTEMENT concourants.
ah,bien joué. ça, je n'avais pas remarqué !!
on peut écrire une contrainte pour que ces trois cercles concourent:
on obtient facilement (trigo+cosinus+al-kashi) les coordonnées
des projetés orthogonaux
donnant une condition nécessaire et suffisante de concourance.
La concourance étant équivalente à une linéarité projective (cf géométrie projective)
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 34 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :