Dérivé
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
femidas
- Membre Naturel
- Messages: 13
- Enregistré le: 26 Jan 2009, 21:40
-
 par femidas » 24 Mar 2009, 21:45
par femidas » 24 Mar 2009, 21:45
Bonsoir
Je dois étudier une fonction mais je ne vois pas du tout comment faire pour la dérivé . Pourriez vous m'aider ? Merci
La voici : f(x) = x/(x-1)(x-4)
-
axiome
- Membre Rationnel
- Messages: 883
- Enregistré le: 04 Mai 2006, 21:37
-
 par axiome » 24 Mar 2009, 21:48
par axiome » 24 Mar 2009, 21:48
Bonsoir,
La formule de la dérivée d'un quotient
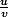
est :

-
femidas
- Membre Naturel
- Messages: 13
- Enregistré le: 26 Jan 2009, 21:40
-
 par femidas » 24 Mar 2009, 21:54
par femidas » 24 Mar 2009, 21:54
axiome a écrit:Bonsoir,
La formule de la dérivée d'un quotient
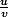
est :

Bonsoir le dénominateur doit donc etre
((x-1)(x-4))² ? c'est ça ?
-
axiome
- Membre Rationnel
- Messages: 883
- Enregistré le: 04 Mai 2006, 21:37
-
 par axiome » 24 Mar 2009, 22:06
par axiome » 24 Mar 2009, 22:06
Exactement.
-
axiome
- Membre Rationnel
- Messages: 883
- Enregistré le: 04 Mai 2006, 21:37
-
 par axiome » 24 Mar 2009, 22:07
par axiome » 24 Mar 2009, 22:07
que tu peux écrire (x-1)²(x-4)² si tu es allergique aux parenthèses...
-
femidas
- Membre Naturel
- Messages: 13
- Enregistré le: 26 Jan 2009, 21:40
-
 par femidas » 24 Mar 2009, 22:33
par femidas » 24 Mar 2009, 22:33
axiome a écrit:que tu peux écrire (x-1)²(x-4)² si tu es allergique aux parenthèses...
Est ce que ceci est bon ?
f '(x)= [(x-1)(x-4)] - (x)/ [(x-1)(x-4)] ²
merci
-
oscar
- Membre Légendaire
- Messages: 10024
- Enregistré le: 17 Fév 2007, 20:58
-
 par oscar » 24 Mar 2009, 22:45
par oscar » 24 Mar 2009, 22:45
Bonsoir
f(x) = x/ (x-1)(x-4) ou x / ( x² -5x+4)
u' = 1 et v' = 2x-5
f' =[ (x²-5x +4) - x ( 2x-5) ]/ ( x-1)² (x-4)²
on peut réduire le numérateur pour trouver les racines
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 34 invités
