Etude de fonction logarithme

par **rich93** » 27 Fév 2009, 15:12

Bonjour j'ai besoin d'aide pour cet exercice d'etude de fonction

1.Calculer f'(x) et étudier son signe sur

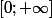
. En deduire le sens de variation de f sur

.

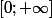
J'ai trouvé

et c'est toujours négatif donc f(x) est strictement décroissante sur l'intervalle

.

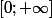
2. Déterminer les limites de f en

et en 0

J'ai trouvé

et

.

3. Montrer que pour tout x element de l'intervalle I=[0.7;0.9], f(x) est aaussi element de I et que |f'(x)|

0.9

Merci pour votre aide

par **makelele** » 27 Fév 2009, 15:17

ba tu bloque ou?

par **rich93** » 27 Fév 2009, 15:22

makelele a écrit:ba tu bloque ou?

Desole j'ai oublie de preciser mais je n'arrive pas la question 3 completement bloque et j'ai aucune idee par ou commencer :cry:

.

par **makelele** » 27 Fév 2009, 15:29

ba tu calcule f(0,7) et f(0,9) (a la calculette je pense pas que tu puisse faire autrement.
tu montre que les deux appartiennent à I.
et comme ta fonction est continue,c'est que pour tout x appartenant à I f(x) appartient aussi à I.
la question de la valeur absolue découle immédiatement après

par **rich93** » 27 Fév 2009, 15:34

makelele a écrit:ba tu calcule f(0,7) et f(0,9) (a la calculette je pense pas que tu puisse faire autrement.
tu montre que les deux appartiennent à I.
et comme ta fonction est continue,c'est que pour tout x appartenant à I f(x) appartient aussi à I.
la question de la valeur absolue découle immédiatement après

ca veut dire que pour |f'(x)| je calcule |f'(0.7)| et |f'(0.9)| qui doivent normalement etre inferieur ou egale a 0.9 et je dis que comme la fonction est continue alors tout ce qui dans l'intervalle [0.7;0.9] est inferieur ou egale a 0.9

C'est ca ?

par **Skullkid** » 27 Fév 2009, 15:43

Salut, je ne suis pas d'accord avec toi pour les questions 1 et 2. Rien ne te choque dans ton expression de f'(x) et dans la limite de f en 0 que tu as trouvées ?

par **rich93** » 27 Fév 2009, 15:57

salut skullkid desole j'ai fait une erreur de frappe sur f(x) que je viens de recorriger et la normalement c'est correct ce que j'ai mis

par **Skullkid** » 27 Fév 2009, 16:19

Ok, plus de souci pour les questions 1 et 2 alors :)

Pour la question 3, pour montrer que f(x) est dans I pour tout x de I, il te suffit en effet de montrer que f(0,7) et f(0,9) sont dans I. Mais ce n'est pas vrai pour toutes les fonctions continues. Quelle propriété supplémentaire de f te permet de faire ça ?

par **rich93** » 27 Fév 2009, 16:48

Skullkid a écrit:Ok, plus de souci pour les questions 1 et 2 alors

Pour la question 3, pour montrer que f(x) est dans I pour tout x de I, il te suffit en effet de montrer que f(0,7) et f(0,9) sont dans I. Mais ce n'est pas vrai pour toutes les fonctions continues. Quelle propriété supplémentaire de f te permet de faire ça ?

Elle est continue et strictement decroissante c'est ca ?

par **Skullkid** » 28 Fév 2009, 02:16

Voilà (monotone dans le cas général). Ensuite la majoration de |f'(x)| tu dois pouvoir l'obtenir avec des minorations sur x et x+1, je vois pas de méthode plus "astucieuse" a priori...

par **rich93** » 28 Fév 2009, 13:31

ok merci beaucoup

Etude de fonction logarithme

etude de fonction logarithme

Qui est en ligne