Suites et Stats

[D3XT3R]

Bonjour,

Je suis nouveau sur ce forum et j'aimerais votre avis sur ce probleme.

Ce n'est peut'etre rien pour la plupart des memebres, mais je galère la dessus:

"Soit la suite des nombres impairs (le premier de ces nombres est1).
a) exprimer, en fonction de n, le nieme de ces nombres
b) determiner la moyenne arithmetique des nombres de cette suite
c) determiner leur variance"

Voila c'est une serie de ce genre d'exercice que j'ai a faire et je ne comprends pas comment faire.

Quelqu'un pourait-il m'aider?

[greg78]

Bonjour,

Pour la premiere question, il faut essayer de regarder pour différents nombres impairs comment on peut les écrire en fonction d'autre chose.
Eg, 1=2*0+1 3=2*1+1 5=2*2+1 etc. D'où la formule pour le n-ième nombre impair.

Pour la seconde question, connais tu la formule de moyenne arithmétique ? Si oui, il suffit de calculer avec l'expression des termes impairs.

[D3XT3R]

J'ai trouve 1+2n pour la a), mais apres je comprends pas comment l'utiliser dans la formule de la moyenne arithmetique:
qu'est-ce que Ni dans ce cas? et Xi? et N? Est-ce des veleur connue, ou des expressions, parceque on ne sait pas combien de termes il y a?

Desole si ca vous semble nul, mais j'a vraiment du mal a raisoner en maths.

[greg78]

On veut calculer la moyenne arithmétique de ces nombres. C'est à dire calculer la moyenne de n nombres impairs.
On va donc sommer les termes qui sont les (2*k+1) pour k entier dans [0,n]. Et on va diviser cette somme par le nombre de termes.
Est ce plus clair ?

[D3XT3R]

On veut calculer la moyenne arithmétique de ces nombres. C'est à dire calculer la moyenne de n nombres impairs.
On va donc sommer les termes qui sont les (2*k+1) pour k entier dans [0,n]. Et on va diviser cette somme par le nombre de termes.
Est ce plus clair ?

Ok, je vois, donc:
J'avais trouvé: sigma de (1+2n) divise par N. Est-ce tout ce qu'on peut faire pour la moyenne?

[greg78]

Soit la moyenne des n premiers termes de notre suite.

On a donc :
D'où
S'il je ne me trompe pas, on a notre résultat.

[D3XT3R]

Ne serait-ce pas k=1 dans le sigma, puisque le 1er nombre est 1 selon l'éconcé. Et aussi ne serait-ce pas plutot Ki ou Xi?

[greg78]

Bonjour,

Non, c'est bien k=0 et non k=1 car le premier terme est 1, et pas 3.

Par contre, il y a quand meme une erreur dans ce que j'ai écrit.
En faisant on somme en fait les n+1 premiers termes et on a donc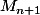

Pour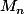 on a donc
D'où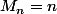

Et sinon pourquoi veux tu absolument avoir des Ki ou des Xi dans la moyenne ?

[D3XT3R]

C'est juste la facon dont c'est ecrit dans mon cours. Si je ne me trompre Ki se refere a l'ensemble des K.

Merci pour ta réponse en tout cas ca m'a aidé.