Bonjour,
Voilà mon problème:
J'ai: [TEX]ln(1+x)<' .
Une idée?
Merci!
Suites et récurrence - Ts
11 messages
- Page 1 sur 1
par uztop » 14 Fév 2009, 16:57
Bonjour,
si cette relation est prouvée:=ln(1+\frac{1}{2})+ln(1+\frac{1}{2^2})+ln (1+\frac{1}{2^3})[...]+ln(1+\frac{1}{2^n}))
Alors, c'est évident: il suffit d'appliquer l'inégalité à chacun des membres:
 \leq \frac{1}{2}))
 \leq \frac{1}{2^2}))
...
 \leq \frac{1}{2^n}))
Et on retombe sur l'expression de Sn
si cette relation est prouvée:
Alors, c'est évident: il suffit d'appliquer l'inégalité à chacun des membres:
...
Et on retombe sur l'expression de Sn
par Leo M » 14 Fév 2009, 19:20
Merci beaucoup! J'ai compris votre raisonnement, je vois le principe, mais comment le démontrez-vous? Par récurrence ou en l'admettant?
par Leo M » 15 Fév 2009, 13:01
Up!
Je comprends le principe mais je ne parviens pas à finaliser la démonstration :/ .
J'avais aussi essayé de faire
, ça pourrait fonctionner selon vous??
Merci!!
Je comprends le principe mais je ne parviens pas à finaliser la démonstration :/ .
J'avais aussi essayé de faire
Merci!!
par uztop » 15 Fév 2009, 16:32
en fait, il suffit d'appliquer l'inégalité pour chaque membre de la somme dans =ln(1+\frac{1}{2})+ln(1+\frac{1}{2^2})+ln (1+\frac{1}{2^3})[...]+ln(1+\frac{1}{2^n}))
Pour)
, on l'utilise pour 
,
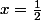
Pour)
, on l'utilise pour 
,
et ainsi de suite.
Etant donné que l'inégalité est vraie pour tout x, on peut l'appliquer à chaque terme de l'inégalité sans aucun problème.
On obtient donc
 \leq \frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}[...]+\frac{1}{2^n})
soit  \leq \s_n)
Pour
Pour
et ainsi de suite.
Etant donné que l'inégalité est vraie pour tout x, on peut l'appliquer à chaque terme de l'inégalité sans aucun problème.
On obtient donc
par Leo M » 15 Fév 2009, 19:18
A d'accord, je ne voyais pas comment rédiger la démonstration!
J'ai un autre problème, pour exprimer Sn en fonction de n; je ne trouve pas de formule qui fonctionne ><' .
J'ai un autre problème, pour exprimer Sn en fonction de n; je ne trouve pas de formule qui fonctionne ><' .
par uztop » 15 Fév 2009, 21:38
il s'agit de la somme des termes d'une suite géométrique; quelle est sa raison ?
par Leo M » 16 Fév 2009, 10:03
Et bien... Le nombre de termes varie en fonction de n; et sa raison aussi!
(Je n'ai vu les raisons que pour les suites arithmétiques et géométriques).
(Je n'ai vu les raisons que pour les suites arithmétiques et géométriques).
par Leo M » 16 Fév 2009, 13:19
A si c'est bon, j'ai compris!
Mais j'ai maintenant un problème pour en déterminer la limite (de Sn)...
Mais j'ai maintenant un problème pour en déterminer la limite (de Sn)...
par uztop » 16 Fév 2009, 13:48
Pour trouver la limite, il faut constater que |q|<1 (q est la raison)
On a donc
On a donc
11 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 50 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :