Vecteurs

[azertyjtm]

bonjours à tous,

Besoin d'aide pour un exercice SVP :
Soit un cercle de centre O, de rayon R et M un point n'appartenant pas à ce cercle
1) Une droite passant par M rencontre (C) en A et B. On désigne par E le point diamétralement opposé à A sur (C).

Montrer que

Déduire que dans chacune des configurations ci-contre, on a



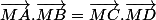
Mercipour votre aide :happy2:

[azertyjtm]

Personne? :(

[oscar]

BONJOUR

Cer'cle O , point M extérieur (ou intérueur ) au cercle
Par définitionV MA*VMB = est la "puissance " de M par rapport au cercle
On a aussiV MA*VMB =V MA*VME si E est diamétalement opposé à A
La sécante ME coupe le cercle en point A' tel que VMA'*VME = VMA*VME

Soit La sécante passant par O, VMC*VMD = (MC+OC)(MC-OC) = MO² -R²
On a la configuration généraleV MA*VMB=V MC*VMD

MO représente la DISTAnCE D' un point au centre du cercle

[azertyjtm]

Tout d'abord, merci,

Le probème est que la notion puissance n'a pas encore été abordée...

[oscar]

Voici la figure: considére cette "puissance" comme un produit de vecreurs
déterminés sur un cercle


http://img178.imageshack.us/my.php?image=pointextrieuraucercleeo4.jpg

[azertyjtm]

Ok merci =)

Je pense qu'une autre méthode me conviendrai mieux et je pense l'avoir trouvée mais il me manque quelques explications ...

=


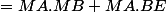
Or ( mais pourquoi ?)

Donc

[azertyjtm]

j'ai trouver la comment du pourquoi :we: :id:

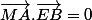
Or on a (MA) perpendiculaire à (EB) on a donc . En effet, [AE] est l'hypoténuse dans le triangle ABE et A, B, E sont des points du cercle donc le triangle ABE est rectangle en B donc on a [MA] perpendiculaire à [EB]

[azertyjtm]

sa coince pour la deuxième question help please :/

[oscar]

RE


Précise ta question..; ta difficulté.

[azertyjtm]

Déduire que dans chacune des configurations ci-contre, on a



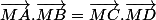
Merci pour votre aide

[azertyjtm]

Tjr personne :'( ?

[azertyjtm]

Aidez moi s'il vous plait je suis en total galère