Suites de Cauchy

[Jissy]

Bonjour à tous !

J'ai un exo sur les suites de cauchy et je bloque sur deux questions...

ENONCE:

On dit que Un est une suite de cauchy lorsque quelquesoit e>0 il existe no appartenant a N tq Quelquesoit(p,q) >(ou egal) à no : l u(p) - u(q) l <(ou egal) e

(p et q etant en indice)

1)(question propsoant de montrer que si Un est convergente alors Un suite de Cauchy déjà traité)

2) On considere Un une suite de Cauchy de nbre réels.

(>)Montrer que Un est bornée ( COMMENT faire?)

(>)il faut en deduire qu il existe une suite extraite qui converge vers l ( il suffit d'utiliser le theorme de bolzano weirestrass)

(>) Montrer que Un converve vers l (je n'y arrive pas non plus)

Donc c'est pour les (>) 1 et 3 que je bloque...merci de bien vouloir m aider.

[Antho07]

ecrit ce que donne la définition de la suite de cauchy avec (par exemple)

Cela te fournit un (le rang à partir duquel |up-uq|<1)

Essaye de voir ce qui se passe pour (


EDIT: pour la question montrer qu'une suite de cauchy est bonrnée j'avais pas précisé désolé

[Antho07]

Arrives-tu à quelque chose?

[Antho07]

Je commence le raisonnement

Soit


Puisque est de cauchy




En particulier,

donc



Par quoi pourrait-on borner U maintenant?

[Jissy]

Je commence le raisonnement

Soit


Puisque est de cauchy




En particulier,

donc



Par quoi pourrait-on borner U maintenant?

Salut Antho007 et merci de ton aide !
Desolé de pas avoir repondu plus tot, ce n'est pas que je n'y arrivais pas, mais je m etais absenté tout en restant connecté sur le forum.

Deja : j'ai du mal a comprendre comment tu arrive dans ton "En particulier" a remplacer l'indice q par n1...

De plus : a la ligne d'en dessous, pourquoi les valeur absolu sont gardé ?
Puisque
lUp-Un1l directement Un1 -1 <(ou egal) Up <(ou egal) Un1 +1 ...
ce qui montre alors que la suite est borné

[Antho07]

-Dans la définition au lieu de prendre p et q quelconque > 1
on prend q=n1 et p quelconque



-


Donc




- Ensuite non , on peut pas borner par

On a pour tout

on sait rien avant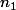

Cependant par quoi pourrait t-on bornée la suite ?
Essaye de représenter les points de la suite sur un dessin sachant que apres n1 c'est bornée

[muse]

Pour les valeur absolue tu peux les garder ou les enlever les deux sont bon.
Pour son "en particulier" il fixe q en fait. Du coup Un1 est fixé du coup 1+Un1 est fixé c'est un nomre. Et tu as a la fin
|Up|<1+Un1 pour pour quelque soit p>n1 donc Up est bornée a partir du rand n1 mais tu sais que si une suite est bornée a partir d'un certain rang alors elle est bornée partout

[Jissy]

Je crois avoir une idée :

On a quelquesoit p superieur ou egal a n1 :
lUp l < 1 + lUn1l
de plus lUp l < 1 + lU(n1-1)l..........lUp l < 1 + l U0l

donc lUp l < max(lU0l,.......l U(n1-1) l, lUn1l +1)
Don la suite est majorée..
Cependant, els valeur absolu me gene assez...je peuc conclure ensuite en disant que Up < max(U0,.......,U(n1-1),Un1 +1) ?

[Antho07]

Je crois avoir une idée :

On a quelquesoit p superieur ou egal a n1 : lUp l < 1 + l Un l

oui et ....


EDIT: c'est 1+ |Un1|

[Antho07]

Vois-tu pourquoi on ne peut pas borner par ?

[Jissy]

Vois-tu pourquoi on ne peut pas borner par ?

As-tu lu mon message precedent ? lol
Je l'ai modifié car dans celui d'origine, en voulant sauter une ligne et donc apres avoir cliqué sur "entrer" je me suis retrouvé avec un message d'une ligne posté....d'ou la rectification juste apres.

[Antho07]

As-tu lu mon message precedent ? lol
Je l'ai modifié car dans celui d'origine, en voulant sauter une ligne et donc apres avoir cliqué sur "entrer" je me suis retrouvé avec un message d'une ligne posté....d'ou la rectification juste apres.

ok

oui c 'est ça




où

[muse]

on s'en fiche un de savoir la valeur de M.
a partir du moment ou on a Up<1+Un1 c'est fini ...

EDIT: en plus on ne pas vraiment qu'elle est la valeur de M puisque deja c'est un max et en plus on connait rien de n1... on ne sait pas s'il est grand petit trse grand tres petit ...

[Antho07]

on s'en fiche un de savoir la valeur de M.
a partir du moment ou on a Up<1+Un1 c'est fini ...

EDIT: en plus on ne pas vraiment qu'elle est la valeur de M puisque deja c'est un max et en plus on connait rien de n1... on ne sait pas s'il est grand petit trse grand tres petit ...

Montrer qu'une suite est bornée , c'est trouver un M tels que



Après si tu dis, puisque la suite est bornée à partir d 'un certain rang , alors elle est bornée .
D'accord mais il faut le montrer, ce que j'ai écris en est la preuve

[Jissy]

Ok super, merci antho07 pour ta patience et tes explications !
Merci à toi aussi muse pour ton aide ;)..

Il me reste alors à montrer que Un converge vers l...Une petite idée pour cette question? :s

[muse]

Montrer qu'une suite est bornée , c'est trouver un M tels que



Après si tu dis, puisque la suite est bornée à partir d 'un certain rang , alors elle est bornée .
D'accord mais il faut le montrer, ce que j'ai écris en est la preuve

Si suite est bornée à partir d 'un certain rang , alors elle est bornée .
Propriété vu au lycée

[Antho07]

Le theoreme de Bolzano Weierstrass te fournit une sous suite convergente .

Soit cette sous suite et l sa limite.

Soit

il faut montrer


est de cauchy








Or est strcitement croissante (définition de sous suite)
donc



En prenant , on a

[Antho07]

Si suite est bornée à partir d 'un certain rang , alors elle est bornée .
Propriété vu au lycée

Il n'empeche que le remontrer n'est pas inutile et permet de bien comprendre ce qui se passe.

[Antho07]

Pour info,
Cet exercice a permit de montrer que dans , toutes les suites de Cauchy convergent.

On dit que est complet.

Espace (métrique) complet= Espace ou toutes les suites de Cauchy convergent