Dm de maths

[liiisou]

Bonjour,
j'ai un exercice à faire et je bloque sur une question:

SABCD est une pyramide régulière de base carrée, de sommet S, de hauteur h et pour laquelle SA=12.

1.a. calculer AB en fonction de h.
1.b. démontrer que le volume de la pyramide est défini par:
V(h)= -2/3h^3+96h avec 02.a. pour quelle valeur de h ce volume est-il maximal? (on pourra
étudier les variations de la fonction V pour h appartenant [0;12]).
2.b. en déduire la valeur du volume correspondant.

1.a. j'ai trouvé : AB = racine de (-2h²+288).
1.b. en utilisant la formule : volume = (aire de la base*hauteur)/3
je trouve la bonne réponse.
2.a. j'ai trouvé la fonction dérivée de la fonction V qui est : V'(h) = -2h²+96 mais que dois-je faire maintenant???

Merci.

[guigui51250]

il faut que tu étudie le signe de la dérivée pour en déduire les variations de la fonction de départ. Avec les variations tu véras le maximun de V

[snakebirds]

Il n'y a pas forcément à étudier les variations (sauf si la fonction admet plusieurs extremums sur différents intervalles). En général (notamment en physique) pour mettre en évidence un maximum on résous l'équation: V'(h)=0 d'inconnue h. Tu trouvera immédiatement la réponse a la question.

Ca te donne: -2h²+96=0
donc h²=48 or h>=0 donc h=racine(48).

Sinon si tu veux faire les variations sur [0;12]:
V'(h)=-2h²+96
Pour h<=racine(48), V'>=0 donc V croissante sur [0;racine(48)]
Pour h>=racine(48), V'<=0 donc V décroissante sur [racine(48);12]
On remet donc bien en évidence un maximum pour V en racine carrée de 48.

[liiisou]

merci beaucoup pour votre aide mais pourquoi utilise-t-on la fonction dérivée et non pas la fonction initiale ???

de plus quand je remplace h par racine de (48) dans la fonction dérivée je trouve 0 est-ce normal ????

[liiisou]

??????????????

[Le Chaton]

merci beaucoup pour votre aide mais pourquoi utilise-t-on la fonction dérivée et non pas la fonction initiale ???

de plus quand je remplace h par racine de (48) dans la fonction dérivée je trouve 0 est-ce normal ????

Bonjour,
Le principe de la dérivée c'est de trouver les variations et les extremum d'une fonction ( une dérivée est nulle a un extremum de la fonction )
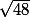
Donc oui c'est normal de trouver 0 si tu remplace h par dans la dérivée.
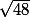
Par contre si tu remplaces h dans ta fonction initiale par tu trouveras l'extremum ...

[liiisou]

Merci beaucoup pour votre aide.

Je trouve donc que l'extremum est : 256 racine de (3) est-ce bien ceci ???

Donc la valeur de h pour que le volume soit maximal est 256 racine de (3) ???

[liiisou]

?????????????????????

[Le Chaton]

Merci beaucoup pour votre aide.

Je trouve donc que l'extremum est : 256 racine de (3) est-ce bien ceci ???

Donc la valeur de h pour que le volume soit maximal est 256 racine de (3) ???

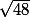
Non la valeur de h pour que le volume soit maximal c'est par contre le volume maximum que tu peux obtenir c'est

[liiisou]

d'accord merci pour votre aide.