Fonction test
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
road runner
- Membre Relatif
- Messages: 163
- Enregistré le: 05 Fév 2007, 18:35
-
 par road runner » 10 Nov 2008, 18:33
par road runner » 10 Nov 2008, 18:33
bonsoir a tous
comment montrer que
={ 1 \text{ si } |x| \le 1 \\ 0 \text{ si } |x| \ge 2)
appartient a
)
merci d'avance
-
road runner
- Membre Relatif
- Messages: 163
- Enregistré le: 05 Fév 2007, 18:35
-
 par road runner » 10 Nov 2008, 18:57
par road runner » 10 Nov 2008, 18:57
j'ai oublié de preciser, que f(x) est comprise entre 0 et 1
merci encore
-
charlol
- Membre Naturel
- Messages: 66
- Enregistré le: 29 Juin 2008, 11:33
-
 par charlol » 10 Nov 2008, 19:27
par charlol » 10 Nov 2008, 19:27
c'est quoi D(IR)?
-
road runner
- Membre Relatif
- Messages: 163
- Enregistré le: 05 Fév 2007, 18:35
-
 par road runner » 10 Nov 2008, 19:45
par road runner » 10 Nov 2008, 19:45
dans la serie de td, c'est dit comme ca, c'est pour ca que ca m'fait un peu tiquer, ca pourait etre ca, oui, dans ce cas, je procede comme pour la suite regularisante ?
merci encore
-
road runner
- Membre Relatif
- Messages: 163
- Enregistré le: 05 Fév 2007, 18:35
-
 par road runner » 11 Nov 2008, 18:39
par road runner » 11 Nov 2008, 18:39
bonsoir, en fait la question est effectivement, montrer qu'il existe une fonction appartenant a D(R^n) qui vérifie ce qui est donnée,
si quelqu'un a une idée,
merci d'avance
-
road runner
- Membre Relatif
- Messages: 163
- Enregistré le: 05 Fév 2007, 18:35
-
 par road runner » 14 Nov 2008, 18:08
par road runner » 14 Nov 2008, 18:08
toujours pas de pistes ? :)

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 14 Nov 2008, 18:09
par leon1789 » 14 Nov 2008, 18:09
road runner a écrit:bonsoir a tous
comment montrer que
={ 1 \text{ si } |x| \le 1 \\ 0 \text{ si } |x| \ge 2)
appartient a
)
merci d'avance
>, avec un
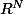
???
-
road runner
- Membre Relatif
- Messages: 163
- Enregistré le: 05 Fév 2007, 18:35
-
 par road runner » 14 Nov 2008, 18:32
par road runner » 14 Nov 2008, 18:32
oui, il faut montrer qu'il existe une fonction f appartenaant a D(Rn) qui verifie ce qui précède
merci encore
-
road runner
- Membre Relatif
- Messages: 163
- Enregistré le: 05 Fév 2007, 18:35
-
 par road runner » 14 Nov 2008, 19:10
par road runner » 14 Nov 2008, 19:10
pourquoi a t-on h(x)=1 quand x est supérieur a 1 ? puisque le supp de g est égale [0,1] ?
-
road runner
- Membre Relatif
- Messages: 163
- Enregistré le: 05 Fév 2007, 18:35
-
 par road runner » 14 Nov 2008, 19:26
par road runner » 14 Nov 2008, 19:26
oui, merci,
sinon est ce que ca ne vous fait pas penser a une fonction plateau, on pourrait utiliser le même raisonnement, non ?
-
road runner
- Membre Relatif
- Messages: 163
- Enregistré le: 05 Fév 2007, 18:35
-
 par road runner » 14 Nov 2008, 19:41
par road runner » 14 Nov 2008, 19:41
d'accord, donc je propose de dire directement, sachant qu'il existe sur un compact K ,d'un ouvert A, une fonction valant 1 sur un voisinage de K
mais cette fonction appartient a D(A) n'est pas ? donc comment généraliser ça à Rn
merci encore
-
road runner
- Membre Relatif
- Messages: 163
- Enregistré le: 05 Fév 2007, 18:35
-
 par road runner » 14 Nov 2008, 20:16
par road runner » 14 Nov 2008, 20:16
pour la suite on forme la suite de fonction fn(x)=f(x/n) , comment montrer qu'elle est aussi dans D(Rn) ?
-
road runner
- Membre Relatif
- Messages: 163
- Enregistré le: 05 Fév 2007, 18:35
-
 par road runner » 14 Nov 2008, 20:55
par road runner » 14 Nov 2008, 20:55
donc comme composition de fonction elle est C infini, et pour le support, normalement ils sont tous inclus dans [0,1] mais comment le montrer ?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 40 invités