Calculer les sommes
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Anonyme
 par Anonyme » 10 Déc 2005, 21:23
par Anonyme » 10 Déc 2005, 21:23
calculer les sommes:
n (n) k
Sn=somme k( ).x
k=0 (k)
n 2 (n) k
Cn=somme k ( ).x
k=0 (k)
je n'arrive pas à commencer... peut être ça vous semble simple, mais moi je m'y perds...
-
Anonyme
 par Anonyme » 10 Déc 2005, 21:32
par Anonyme » 10 Déc 2005, 21:32
Comment vous écrivez les sommes?
je voulais écrire somme de k=0 à n et touut le reste, mais ça sort pas bien à l'écran...
-
Anonyme
 par Anonyme » 12 Déc 2005, 14:00
par Anonyme » 12 Déc 2005, 14:00
-
Anonyme
 par Anonyme » 12 Déc 2005, 14:09
par Anonyme » 12 Déc 2005, 14:09
ça soit être ma formule, mais je ne sais pas comment la mettre ?
-
rene38
- Membre Légendaire
- Messages: 7135
- Enregistré le: 01 Mai 2005, 11:00
-
 par rene38 » 12 Déc 2005, 15:57
par rene38 » 12 Déc 2005, 15:57
Bonjour

est obtenu par
[T E X]S_n=\Bigsum_{k=0}^nk\(n\\k\)x[/ T E X]
en supprimant les espaces de [T E X] et [/ T E X]
Edit : j'ai oublié l'exposant k à la fin : 
[T E X]S_n=\Bigsum_{k=0}^nk\(n\\k\)x^k[/ T E X]
-
Galt
- Membre Rationnel
- Messages: 789
- Enregistré le: 13 Aoû 2005, 12:03
-
 par Galt » 12 Déc 2005, 20:08
par Galt » 12 Déc 2005, 20:08
En fait, les invités n'ont pas droit à latex. Ils n'ont qu'à s'inscrire. Bien fait pour eux
-
roni65
- Messages: 7
- Enregistré le: 12 Déc 2005, 21:26
-
 par roni65 » 12 Déc 2005, 21:36
par roni65 » 12 Déc 2005, 21:36
rene38 a écrit:Bonjour

est obtenu par
[T E X]S_n=\Bigsum_{k=0}^nk\(n\\k\)x[/ T E X]
en supprimant les espaces de [T E X] et [/ T E X]
Edit : j'ai oublié l'exposant k à la fin : 
[T E X]S_n=\Bigsum_{k=0}^nk\(n\\k\)x^k[/ T E X]
Merci! je teste :
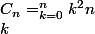x^k)
yes
 Merci beaucoup!
Merci beaucoup! ça marche

-
roni65
- Messages: 7
- Enregistré le: 12 Déc 2005, 21:26
-
 par roni65 » 12 Déc 2005, 21:39
par roni65 » 12 Déc 2005, 21:39
Galt a écrit:En fait, les invités n'ont pas droit à latex. Ils n'ont qu'à s'inscrire. Bien fait pour eux
C'est fait Monsieur :zen: !
Si je m'inscris à chaque forum..... je vais m'y perdre. Je voulais voir comment ça fonctionne et si on a des bonnes réponses

, donc me voilà inscrite!
-
Nicolas_75
- Membre Rationnel
- Messages: 919
- Enregistré le: 29 Aoû 2005, 11:42
-
 par Nicolas_75 » 13 Jan 2006, 15:51
par Nicolas_75 » 13 Jan 2006, 15:51
Bonjour,
^n=\bigsum_{k=0}^n{n\choose k}x^k)
En dérivant par rapport à x, et en multipliant par x, on obtient :
^{n-1}})
En dérivant par rapport à x, et en multipliant par x, on obtient :
(1+x)^{n-2}})
Sauf erreur.
Nicolas
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 31 invités


