Irrationnalité V2

[theboss]

J'ai cet exercice que je ne comprends vraiment pas, si vous pouvez m'aider à démarrer ce serait gentil de votre part. Je compte sur votre aide. Merci.


Problèmes historiques sur les nombres, irrationnalité de V 2, ...
On se propose de démontrer que V2 est un irrationnel.

1.Préambule

a désigne un entier naturel. Démontrer que :
a) Si a est pair, alors a² est pair ;
b) Si a est impair, alors a² est impair.

2. Démonstration de l'irrationnalité de V2

On utilise un raisonnement par l'absurde.
On suppose donc que V2 est rationnel, c'est-à-dire qu'il existe des entiers naturels a et b, avec b différent de zéro, tels que
V2 = (a/b) où a/b est une fraction irréductible.
a) Vérifier qu'alors a²= 2b².
b) Quelle est donc la parité de a² ?
Déduire du préambule que a est pair.
c) On pose a = 2a' avec a' appartient à N ( ensemble de nombre naturel)
Démontrer qu'alors b' - 2a'² et en déduire que b est pair.
d) Déceler où se situe la contradiction en utilisant l'hypothèse et les questions b) et c).
e) En déduire que V2 est irrationnel.

[leon1789]

Pourquoi toujours dire que c'est une preuve par l'absurde alors qu'il s'agit d'une preuve directe du fait :

pour tout entier naturel, est soit entier, soit irrationnel.

(ce qui démontre instantanément que sont irrationnels puisque non entiers...)
???

[Kah]

Non leon1789! Pour tout entier naturel n, Vn est soit entier, soit irrationnel, soit une fraction.
La, il s'agit de prouver que V2 ne peut s'ecrire sous forme de fration.

[Zweig]

Faux Kah : si , alors ou . En aucun cas :

On va montrer que () est soit entier soit irrationnel

Supposons que est rationnel. Soit la valuation p-adique de l'entier .

Nous avons, compte tenu du fait que :



ou encore

car est un nombre entier. D'où .

[Zweig]

Démo : On va montrer que () est soit entier soit irrationnel

Supposons que est rationnel. Soit la valuation p-adique de l'entier .

Nous avons, compte tenu du fait que :



ou encore

car est un nombre entier. D'où .

[leon1789]

Autre preuve de rationnel => entier :

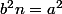
Si est rationnel, alors avec . Donc , et donc b² divise a², donc b² divise . Or , donc b² divise 1 , donc , donc est entier.

Mais là, c'est de ma faute, on fait du hors sujet...

[Kah]

:zwip: mais on adore. 5/8 n'est pas un entier naturel, mais n'est pas irrationel non?

[Zweig]

Certes, mais , or ici le nombre sous le radical est un entier naturel.

[Kah]

Vn rationnel--->n entier??
Heu y a pas un raccourci de pris?

[leon1789]

:zwip: mais on adore. 5/8 n'est pas un entier naturel, mais n'est pas irrationnel non?

ok, mais 5/8 n'est la racine carré d'aucun entier, si ? :we:

[leon1789]

soit un entier naturel, si est rationnel alors est entier.

pour tout entier naturel, est soit entier, soit irrationnel.

je ne vois pas de raccourci particulier :zen:

[Kah]

Ok j'ai compris merci! :id: