Limites avec racine

[snoopye68]

Bonjour à tous,

Je "sèche" devant un calcul de limites...
J'ai tenté la quantité conjugué, mais je reste toujours devant une forme indéterminée...

lim de x qui tend vers 1 de :

( (racine (x+3) ) -2) : ( (racine(x) ) -1)

Merci à celui qui saura me mettre sur la voie!

[le_fabien]

Bonjour ,
le mieux est d'utiliser la dérivabilité en 1 des fonctions
et

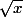
[Flodelarab]

Tu cherches:


Par la quantité conjugué tu trouves qqch de la forme:

Ne serait ce pas la formule de la dérivée de f en 1 ?
Bien sûr que si.


A toi de déterminer f, de la dériver et de calculer sa valeur en 1

[maf]

ou encore, multiplie par le conjugué en haut ... et en bas, il y a alors une simplification qui apparaît ... et du coup la limite n'est plus indeterminée

[Flodelarab]

ou encore, multiplie par le conjugué en haut ... et en bas, il y a alors une simplification qui apparaît ... et du coup la limite n'est plus indeterminée

Je suis curieux que tu m'expliques cela...

[le_fabien]

ou encore, multiplie par le conjugué en haut ... et en bas, il y a alors une simplification qui apparaît ... et du coup la limite n'est plus indeterminée

Bizarre bizarre ! :hum:

[maf]

me serais-je planté ? :marteau:

=

[maf]

si je me suis planté, j'arrive vraiment pas à voir où ... :stupid_in

[Flodelarab]

On a toujours un nuérateur ui tend vers 0 et un dénominateur qui tend vers 0.
Où est le progrès ?

[maf]

il est là le progrès ...

me serais-je planté ? :marteau:

=

x+3-4 = ... x-1 !! Bingo !!!

=
=

YOUPIE

[le_fabien]

me serais-je planté ? :marteau:

=

Cela à l'air bon.

[Flodelarab]

bravo :++:

[maf]

Merci :ptdr:

[snoopye68]

Merci beaucoup!!
:++: Je n'avais pas pensé à la petite astuce...
Je me suis retrouvée avec une expression bien compliquée, et je m'en sortais plus!