Matrice

par **samah** » 06 Juil 2008, 19:18

Salut,
Si on a deux systémes lineaires homogenes ,
et si on nous a dit , soit P une matrice dont les colonnes sont formées par les vecteurs des bases des solutions de ces deux systemes .
ma question est , comment va t on former cette matrice , il y a quatre vecteurs , laquelle on va mettre dans la premiere colonne et laquelle dans la deuxieme ...
si on la forme au hasard c à d sans choisir l'ordre des vecteurs , est ce que ça ne va pas changer les reultats des questions suivantes (

..)

par **rafbh** » 06 Juil 2008, 19:55

Le premier vecteur de la base a la première colonne!

par **samah** » 06 Juil 2008, 20:02

rafbh a écrit:Le premier vecteur de la base a la première colonne!

mais on peut pas donner l'ordre a ces vecteurs ,
supposons qu'on a pu donner lordre aux deux vecteurs de la premiere solution ,
mais on a deux systemes a resoudre , chaque eleve va commencer par un systeme , on peut pas assurer qu'on va tous debuter par le meme systeme

par **Clembou** » 06 Juil 2008, 22:59

samah a écrit:Salut,
Si on a deux systémes lineaires homogenes ,
et si on nous a dit , soit P une matrice dont les colonnes sont formées par les vecteurs des bases des solutions de ces deux systemes .
ma question est , comment va t on former cette matrice , il y a quatre vecteurs , laquelle on va mettre dans la premiere colonne et laquelle dans la deuxieme ...
si on la forme au hasard c à d sans choisir l'ordre des vecteurs , est ce que ça ne va pas changer les reultats des questions suivantes ( ..)

On peut prendre un exemple :

Mettre sous forme matricielle le système suivant :

Tu verras qu'il y a plusieurs façons de construire cette matrice mais si tu précises à droite quelle ordre, tu verras qu'il est plus logique de mettre en premier

, en deuxième

....

Si de plus, tu inverses par exemple la colonne

et la colonne

, pour retrouver la "bonne" matrice inverse, il faudra inverser la colonne des

avec celle des

... Le déterminant (même en inversant deux colonnes) est toujours le même

par **samah** » 06 Juil 2008, 23:04

moi quand je l'ai resolu , je les ai mis selon un ordre à moi , lol , pour me faciliter de trouver une matrice sous forme cannonique afin de trouver P^-1
mais je sais pas si cet ordre va m'enmener au resultat juste

par **samah** » 06 Juil 2008, 23:21

pour le systeme que tu m'as proposé , je vois bien qu'il y a plusieurs façon de construire une matrice , et la plus logique c'est celle que tu as proposée ,
mais est ce que toutes les matrices choisis vont mener au meme resultats

par **Clembou** » 06 Juil 2008, 23:24

samah a écrit:pour le systeme que tu m'as proposé , je vois bien qu'il y a plusieurs façon de construire une matrice , et la plus logique c'est celle que tu as proposée ,
mais est ce que toutes les matrices choisis vont mener au meme resultats

"A permutations près", on a la même matrice

et donc celle de

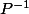
aussi ...

par **samah** » 06 Juil 2008, 23:27

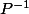
Clembou a écrit:"A permutations près", on a la même matrice et donc celle de aussi ...

on aura pas la meme matrice p
par ex moi je met 2x au debut et toi tu choisis x
alors on aura pas la meme patrice p

Matrice

matrice

Qui est en ligne