Exponentiel de matrice: solution d'un systeme

[fidi]

Bonsoir à tous,

Voilà, je me retrouve devant un "petit" problème que j'avoue avoir du mal à résoudre...

A partir de cette équation fonctionnelle:

M(x+y) = M(x).M(y)
avec M(x) la fonction de transfert d'un tuyau (matrice 2x2).

Si A, B et C désigne 3 sections du tuyau séparé par les distances x et y, on peut lier les vecteurs perturbation P (pression et débit) par:
Pb=M(x).Pa ; Pc=M(y).Pb et Pc = M(x+y).Pa


Comment peut on démontrer que les matrices M(x) solution de l'équation fonctionnelle sont de la forme:
M(x) = exp (x.K)

avec K une matrice (2.2) à coefficients complexes ne dépendant pas de x

Par avance merci

[Aspx]

Dérivabilité automatique :
La multiplication à gauche par étant linéaire et continue elle commute avec l'intégration d'où en intégrant ta relation

[CENTER][/CENTER]
i.e
[CENTER][/CENTER]

Il reste plus qu'à trouver un tel que soit inversible (on aura alors le caractèr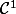e de ). Or (j'imagine que les conditions initiales doivent imposer ) vu continue puis en primitivant le DL
qui est inversible pour assez petit ( ouvert)

On peut dériver (d/dy) :
[CENTER][/CENTER]
Puis
[CENTER][/CENTER]

Fonction auxiliaire :
Posons
[CENTER][/CENTER]
Sa dérivée est nulle, puis la conclusion vient ensuite.

[fidi]

Bonsoir, merci de ta réponse !! Je suis vraiment impressionné par ta rapidité !!! merci. Cependant une chose m'échappe encore comment détermines tu la fonction auxiliaire et comment conclure?

Merci de ces éclairsicements

[Aspx]

Eh bien
[CENTER][/CENTER]

Donc est constant donc

Finalement en multipliant à droite par il vient

[CENTER][/CENTER]

[fidi]

Ok, désolé, je n'avais pas vu qu'il fallait dérivé Q...(mal lu :dodo: )

Je vais me permettre d'abuser un peu:

Je voudrais comprendre comment on arrive à l'expression suivante

Si on pose M'(0) = K



Encore merci pour la réactivité.