Nouveau membre
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
m@riss@
- Membre Naturel
- Messages: 18
- Enregistré le: 21 Mai 2008, 10:57
-
 par m@riss@ » 21 Mai 2008, 11:15
par m@riss@ » 21 Mai 2008, 11:15
bonjour a tous et a toutes :we:
je suis un nouveau membre et j'ai besoin de votre aide,
pouvez vous m'aider svp a résoudre ces limites: :help:
*lim(apuissancex +bpuissancex)puissance1/x
et x tend vers l'infini
*lim (logx)puissance tg(pi x /2e) avc x tend vers e
merci d'avance de m'avoir repondu si vite.
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 21 Mai 2008, 11:43
par yos » 21 Mai 2008, 11:43
Bonjour.
Suppose a>b et mets a^x en facteur.
-
mathelot
 par mathelot » 21 Mai 2008, 11:49
par mathelot » 21 Mai 2008, 11:49
m@riss@ a écrit:merci d'avance de m'avoir repondu si vite.
bonjour,
il faut bien récompenser un tel optimisme :zen:
on considère a>0 et b>0
Pour la question (1), il est possible de prendre le log de la fonction,
on discute selon le cas:
a>b , on met alors
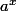
en facteur dans la somme (le terme dominant) et il restera
} ))
que l'on peut développer avec un DL.
-
mathelot
 par mathelot » 21 Mai 2008, 11:55
par mathelot » 21 Mai 2008, 11:55
damned, grillé par Yos !!! :zen:
Pour le (2),
on peut poser
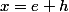
=g(e+h)=ln(e+h) \tan(\frac{\pi}{2}+ \frac{\pi}{2e}h)=<br />\frac{\ln(1+\frac{h}{e})}{ - tan(\frac{\pi h}{2e}) })
plus agréable, non ?
je te laisse conclure.
-
ffpower
- Membre Complexe
- Messages: 2542
- Enregistré le: 13 Déc 2007, 04:25
-
 par ffpower » 21 Mai 2008, 11:55
par ffpower » 21 Mai 2008, 11:55
pas de DL la a priori puisque la limite est en +infini
-
mathelot
 par mathelot » 21 Mai 2008, 11:57
par mathelot » 21 Mai 2008, 11:57
ffpower a écrit:pas de DL la a priori puisque la limite est en +infini
)
,
si on écrit, au voisinage de

=e^{ -x} - 0,5 e^{ -2x}+ \frac{1}{3} e^{ -3x} +o(e^{ -3x}))
comment appelle-t-on cela ?
-
ffpower
- Membre Complexe
- Messages: 2542
- Enregistré le: 13 Déc 2007, 04:25
-
 par ffpower » 21 Mai 2008, 12:23
par ffpower » 21 Mai 2008, 12:23
Soit,tu peux en faire un,mais il est inutile
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 21 Mai 2008, 12:43
par yos » 21 Mai 2008, 12:43
Le logarithme est-il indispensable?
Dans
^x\right)^{\frac1x})
la parenthèse est du 1^0.
-
m@riss@
- Membre Naturel
- Messages: 18
- Enregistré le: 21 Mai 2008, 10:57
-
 par m@riss@ » 21 Mai 2008, 16:41
par m@riss@ » 21 Mai 2008, 16:41
merci pour votre aide
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 69 invités
