Matrice ...

[Mohamed Taoufiq]

bonjour a tous , si vous pouvez me donner des indications ...
1) soit E un k-es de dim n . determiner les endomorphismes de E ayant la meme matrice dans toutes les bases <=> (f tq qu'elles que soient B , B' 2 bases de E , mat(f,B)=mat(f,B') )
2) en deduire les matrices carrées d'ordre n qui commutent avec les matrices inversibles
et merci

[alavacommejetepousse]

bonjour

on pourrait s'attendre à faire 2) puis 1) dans cet ordre

en respectant l'ordre
1)
a) Montrer que pour tout x
(x,f(x)) liée sinon en prenant une base de la forme (e1,e2=f(e1),...)
avec( e1 ,f(e1) ) libre

puis la base (2e1,e2,...)
b)en déduire que f est une homothétie

[Mohamed Taoufiq]

j'ai pas comprit , s'il y a une methode plus simple va etre mieux

[tize]

Bonjour,
Pour passer d'une matrice exprimée dans une base à une autre base il faut multiplier par une matrice inversible :
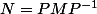avec N et M représente le même endomorphisme dans deux bases différentes.
Dans ton énoncé il est dit que la matrice est la même quelque soit le changement de base donc pour tout , 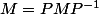c'est à dire 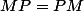pour tout .
On te demande en fait quelle sont les matrices qui commutent avec toutes les matrices inversibles. Ou encore quelle sont les endomorphismes E qui commutent avec tous les automorphismes de E.
Soit u un tel endomorphisme. Suppose qu'il existe e1 non nul dans E tel que (e1,e2) est libre avec e2=u(e1) et complète (e1,e2) en B=(e1,e2,...,en) une base de E.
Considère maintenant l'endomorphisme v tel que v(e1)=e1 et v(e2)=e1+e2 et v(ei)=ei pour i>2, c'est un automorphisme car l'image l'image de B est une base de E et on doit avoir uov=vou.
Montre que c'est impossible et donc que pour un tel endomorphisme u, (x,u(x)) est liée pour tout x dans E donc que .
Ensuite montre que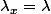 ne dépend pas de x.

[Mohamed Taoufiq]

merci alavacommejetepousse et tize , j'ai compris