Petite dérivée
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
zelda007
- Membre Relatif
- Messages: 164
- Enregistré le: 30 Déc 2007, 15:04
-
 par zelda007 » 19 Fév 2008, 12:58
par zelda007 » 19 Fév 2008, 12:58
Bonjour, dans le cadre d'un devoir, j'ai une petite dérivée à calculer et je bloque :
Soit Bn = Somme(k=0..n)(k parmi n).bk.X^(n-k)
Je dois montrer que la dérivée de Bn vaut : n.B(n-1)
La dérivée d'une somme est la somme des dérivées donc :
(Bn)' = Somme(k=0..n)(k parmi n).bk.(n-k)X^(n-k-1) Mais ensuite je ne vois pas comment arriver au résultat...
Merci
-
prepahec1
- Membre Naturel
- Messages: 21
- Enregistré le: 14 Juil 2007, 15:22
-
 par prepahec1 » 19 Fév 2008, 15:34
par prepahec1 » 19 Fév 2008, 15:34
Essaye de passer par le binome de newton
-
zelda007
- Membre Relatif
- Messages: 164
- Enregistré le: 30 Déc 2007, 15:04
-
 par zelda007 » 19 Fév 2008, 15:45
par zelda007 » 19 Fév 2008, 15:45
Mais ou vois tu un binome de Newton ?

-
fatal_error
- Membre Légendaire
- Messages: 6610
- Enregistré le: 22 Nov 2007, 12:00
-
 par fatal_error » 19 Fév 2008, 16:23
par fatal_error » 19 Fév 2008, 16:23
Bonjour,
N'a-t-on pas
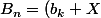^n)
? (le binome de newton comme recommande prepahec1)
Si tel est le cas,
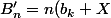^{n-1}=nB_{n-1})
la vie est une fête

-
zelda007
- Membre Relatif
- Messages: 164
- Enregistré le: 30 Déc 2007, 15:04
-
 par zelda007 » 19 Fév 2008, 16:28
par zelda007 » 19 Fév 2008, 16:28
Bah non...
Car (bk + X)^n = somme(k parmi n).(bk)^k.X^(n-k)
Il manque le "puissance k" sur le bk... ou alors je deviens fou :marteau:

-
fatal_error
- Membre Légendaire
- Messages: 6610
- Enregistré le: 22 Nov 2007, 12:00
-
 par fatal_error » 19 Fév 2008, 17:08
par fatal_error » 19 Fév 2008, 17:08
Hum désolé.
bon ben mettons alors qu'on ait tout simplement 1^k
le bk est produit tu peux le sortir de la somme et tu trouves
Bn=b_k(1+X)^n
Apres tu sauras trouver je pense.
la vie est une fête

-
zelda007
- Membre Relatif
- Messages: 164
- Enregistré le: 30 Déc 2007, 15:04
-
 par zelda007 » 19 Fév 2008, 17:32
par zelda007 » 19 Fév 2008, 17:32
non on ne peut pas sortir le bk de la somme car il dépens de k !
-
zelda007
- Membre Relatif
- Messages: 164
- Enregistré le: 30 Déc 2007, 15:04
-
 par zelda007 » 19 Fév 2008, 22:54
par zelda007 » 19 Fév 2008, 22:54
Personne n'a d'idée ?

-
fatal_error
- Membre Légendaire
- Messages: 6610
- Enregistré le: 22 Nov 2007, 12:00
-
 par fatal_error » 20 Fév 2008, 00:01
par fatal_error » 20 Fév 2008, 00:01
Oki, petit idée par la!
Calculons dérivée de Bn:
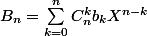
=>
)'=\sum_{k=0}^{n-1} C_n^k b_k (n-k) X^{n-k-1})
(le terme constant est atteint pour k=n, la dérivée le fait péter)
or
C_n^k =(n-k) \frac{n!}{(k!)(n-k)!} =\frac{n!}{(k!)(n-k-1)!})
Calculons

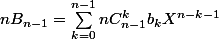
Or
!}{(k!)(n-1-k)!} = \frac{n!}{(k!)(n-k-1)!})
Apres on trouve bien
)'=nB_{n-1})
la vie est une fête

-
zelda007
- Membre Relatif
- Messages: 164
- Enregistré le: 30 Déc 2007, 15:04
-
 par zelda007 » 20 Fév 2008, 21:58
par zelda007 » 20 Fév 2008, 21:58
Merci j'avais fini par trouver ^^
-
zelda007
- Membre Relatif
- Messages: 164
- Enregistré le: 30 Déc 2007, 15:04
-
 par zelda007 » 20 Fév 2008, 22:05
par zelda007 » 20 Fév 2008, 22:05
Erreur message a supprimer
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 16 invités
