J'ai un exercice à faire je m'y suis penché très longtemps je l'ai tourné dans tout les sens mais je comprends vraiment toujours que dalle!!!
Soit f la fonction définie sur R par f(x)=e^(-x2/2)
soit f^(k), k e N, la dérivée kième de f, on pose f^(0)=f.
1) Montrer que pour tout réel x, f^(k) (x)= Hk(x)e^(-x2/2) ou Hk est un polynôme de degré k de même parié que k vérifiant la relation de récurrence:
pour tout reel x: Hk+1(x)= H'k(x)-xHk(x).
Les polynômes Hk portent le nom de polynôme de Hermite.
2) Montrer par recurrence que pour tout n dans N:
H"n(x)-xHn'(x)+nHn(x)=0
Si vous avez des soucis avec l'écriture de l'exercice dites le moi ^^
J'ai vraiment rien de chez rien compris... help meeeee lol
Fonction exponentielle
2 messages
- Page 1 sur 1
la dérivée k ième de f c'est la fonction qu'on obtient en dérivant k fois f
on a=e^{- \frac{x^{2}}{2}})
Il faut montrer que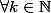
}(x)=H_{k}(x) \times e^{- \frac{x^{2}}{2}})
avec Hk(x) un polynome de parité de k.
Autrement si k est paire alors la fonction polynomiale Hk(x) est paire.
et si k est impaire alors la fonction polynomiale Hk(x) est impaire.
On montre le résulat par récurrence sur la propriété P(k)="}(x)=H_{k}(x) \times e^{- \frac{x^{2}}{2}})
avec Hk(x) un polynome de parité de k."
Initialisation: k=0
alors}(x)=f(x)=e^{- \frac{x^{2}}{2}}=H_{0}(x) \times e^{- \frac{x^{2}}{2}}) avec Ho(x)=1 paire comme 0.
avec Ho(x)=1 paire comme 0.
DOnc P(0) est vrai.
On suppose le résultat vrai à un certain rang k entier. Montrons alors que la propriété est vrai au rang k+1
}(x)=(f^{(k)}(x))'= (H_{k}(x) \times e^{- \frac{x^{2}}{2}})') par hypothese de récurrence.
par hypothese de récurrence.
Dérivons:
}(x)=H_{k}'(x)\times e^{-\frac{x^{2}}{2}}-xH_{k}(x)e^{-\frac{x^{2}}{2}}=(H_{k}'(x)-xH_{k}(x))e^{-\frac{x^{2}}{2}}=H_{k+1}(x)e^{-\frac{x^{2}}{2}})
Avec= H_{k}'(x)-xH_{k}(x)) qui est bien un polynome, reste à vérifier sa paraité.
qui est bien un polynome, reste à vérifier sa paraité.
On suppose k paire Hk(x) est paire donc (Hk)'(x) est impaire et xHk(x) est impaire donc (Hk)'(x)-xHk(x) est impaire donc Hk+1(x) est impaire comme k+1.
De meme si k est impaire alors Hk+1(x) est paire comme k +1.
La propriété est vrai au rang k+1 donc pour tout entier.
on a
Il faut montrer que
avec Hk(x) un polynome de parité de k.
Autrement si k est paire alors la fonction polynomiale Hk(x) est paire.
et si k est impaire alors la fonction polynomiale Hk(x) est impaire.
On montre le résulat par récurrence sur la propriété P(k)="
avec Hk(x) un polynome de parité de k."
Initialisation: k=0
alors
DOnc P(0) est vrai.
On suppose le résultat vrai à un certain rang k entier. Montrons alors que la propriété est vrai au rang k+1
Dérivons:
Avec
On suppose k paire Hk(x) est paire donc (Hk)'(x) est impaire et xHk(x) est impaire donc (Hk)'(x)-xHk(x) est impaire donc Hk+1(x) est impaire comme k+1.
De meme si k est impaire alors Hk+1(x) est paire comme k +1.
La propriété est vrai au rang k+1 donc pour tout entier.
2 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 70 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
