Fonction indéterminée+ inéquation

[Mathematic]

Bonsoir tout le monde
Alors voila j'ai deux petit soucis dans un DM:

I)j'essaye de calculé ca:
lim x-->+infini de (1500x+100)/x² ; je tombe donc sur INFINI/INFINI donc une forme indertimiinée
Comment faire? je ne trouve vraiment pas.

II)
On me demande de résoudre l'inéquation suivante:
(1500x+100)/x² < ou égal à 10
Et là je suis vraiment complètement bloqué aussi :mur:
Esperant trouvé de l'aide

III) dernière petite question ou plutot verification sur ma dérivé^^
Lorsque je dérive F(x)=5x+31+(1500x+100)/x² je trouve F'(x)=5 + (-2000x²-200x)/(x²)²
Est ce juste? Et sinon comment calculer F'(x)=0

Merci beaucoup d'avance de toute les aides que vous pourrez me fournir.
Bonne soirée à tous.

[Skullkid]

Bonsoir,

I - Factorise le numérateur et le dénominateur par les puissances de x dominantes (ici, tu factorises en haut par x et en bas par x²) et simplifie. Cette méthode est vue en cours, normalement. Elle est valable pour toutes les fractions rationnelles (quotients de polynômes) en l'infini.

II - Multiplie ton inéquation par x² (qui est positif) et tu tombes sur une inéquation du second degré, que tu es censé savoir résoudre.

III - Je trouve

[Mathematic]

Bonsoir et merci pour vore aide;

-pour le I) je trouve de ce fait + infini alors que je suis censé trouvé 0 (pour démontrer que c'et une asymptote oblique) erreur de calcul de ma part?

-pour le II) il faut bien que je multiplie par X² et ensuite passé le 10 de l'autre coté de facon à trouver: -10x²+1500x+100
- pour le III) je te remercie de ta correction, et alors comment trouvé F'(x)=0?

Bonsoir

[Skullkid]

I - Oui, tu es censé trouver 0 : quand x tend vers l'infini,

II - C'est ça, et tu peux aussi simplifier par 10, ça fait pas de mal

III - Pour F'(x)=0, ça m'a l'air de donner une équation du 3ème degré sans racine évidente, donc a priori je sais pas la résoudre. Tu en as besoin dans ton exo ?

Edit : On peut juste se contenter de prouver l'existence de solutions, mais en donner une expression, ça me paraît difficile.

[Mathematic]

Rebonsoir; en effet j'essaye de trouver F'(x)=0 dans le but de faire le tableau de signe de F'(x) et donc de trouver la valeur ou F'(x) s'annule.
Pourquoi, existe t'il une autre méthode dont je ne me souviens plus, car il est vrai j'ai quelques oublis en ce moment :ptdr:
En tout cas merci beaucoup déjà de votre aide précieuse.

[Skullkid]

Qu'est-ce qui est demandé dans ton exercice ?

On n'a pas toujours accès à la valeur des solutions d'une équation. Soit l'équation est censée avoir des solutions simples (ce qui n'est pas le cas) et dans ce cas il y a peut-être une erreur dans ton énoncé, soit ce qu'on attend de toi c'est juste de déterminer le nombre de solutions de cette équation, et de les situer.

Si l'exercice te demande de dresser le tableau de variations de F, je ne pense pas qu'une résolution numérique de F'(x)=0 soit attendue.

[Mathematic]

Bonjour;
Très bien, merci beaucoup pour toutes ces précisions importantes.
Pour etre un peu plus clair, voila en fait la question que j'ai:

Cm(q)= 5q+31+(1500Q+100)/q² pour q ]0; + infini[

Cm(q) représente le cout moyen lorsquon a fabriqué q centaine d'objets.

ma question: Déterminer le nombre d'objets à produire, à la dizaine près pour avoir un cout moyen minimal.

-----> Pour répondre à cette question j'ai donc voulu chercher la dérivé pour ensuite faire son tableau de signe, afin de finalement faire le tableau de variation de Cm(q) et connaitre son point le plus bas qui serait la réponse à ma question.

Existe t'il un autre moyen, peut être sans avoir recours au tableau de variation de trouver la réponse?

Merci beaucoup

[Skullkid]

Non, c'est bien la bonne méthode, mais on te demande une valeur approchée du nombre d'objets à la dizaine près, donc une valeur à 0,1 près du minimum de F sur .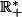

Ce que je te propose de faire pour F', c'est de trouver le nombre de solutions de l'équation F'(x)=0 sur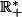 , et de les situer grossièrement (tu peux leur donner un nom, genre 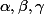etc). Avec ces valeurs tu vas pouvoir tracer le tableau de variations de F, et tu verras ce qui correspond à un minimum pour F.

Une fois que tu auras trouvé le minimum (formellement, tu n'auras pas encore sa valeur approchée), tu vas pouvoir en déterminer une valeur approchée en regardant les valeurs de F' autour du minimum (je sais pas si je suis très clair).

[Mathematic]

Non, c'est bien la bonne méthode, mais on te demande une valeur approchée du nombre d'objets à la dizaine près, donc une valeur à 0,1 près du minimum de F sur .

Ce que je te propose de faire pour F', c'est de trouver le nombre de solutions de l'équation F'(x)=0 sur , et de les situer grossièrement (tu peux leur donner un nom, genre etc). Avec ces valeurs tu vas pouvoir tracer le tableau de variations de F, et tu verras ce qui correspond à un minimum pour F.

Une fois que tu auras trouvé le minimum (formellement, tu n'auras pas encore sa valeur approchée), tu vas pouvoir en déterminer une valeur approchée en regardant les valeurs de F' autour du minimum (je sais pas si je suis très clair).

A vrai dire, tu es peut être clair, mais je suis un peu perdu dans tous ces calculs, je n'ai pas très bien compris car je n'ai jamais été dans cette situation ou les racines ne sont pas évidentes :hein:

[Skullkid]

En ce qui concerne la preuve de l'existence des racines de F', et le fait de trouver celle qui correspond au minimum de F sur 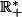, je pense que tu en es capable.

Normalement, tu dois trouver dans un premier temps que le minimum de F sur 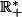est plus grand que 10. Ça ne te suffit pas puisqu'on te demande une approximation à 0.1 près de .

Pour trouver cette valeur approchée, tu vas évaluer F' autour de , je m'explique : tu sais que est le seul réel supérieur à 10 qui vérifie , et que de plus F' est négative avant , et positive après . C'est de ça dont on va se servir pour calculer une valeur approchée de :

Tu calcules par exemple F'(20), tu vas trouver qu'il est positif, tu en déduis donc que est compris entre 10 et 20, c'est déjà mieux, mais ça suffit toujours pas. Alors tu vas calculer F'(15) (tu prends le milieu du segment [10,20]) :

Si F'(15)>0 tu sauras que est compris entre 10 et 15.
Si F'(15)<0 tu sauras que est compris entre 15 et 20.

Et ainsi de suite jusqu'à ce que tu arrives à situer dans un intervalle de longueur inférieure à 0.1, tu auras alors une valeur approchée de à 0.1 près.

Voilà, je pense que c'est plus clair comme ça.