Calcul Spirale

par **buggy** » 23 Oct 2007, 19:30

Bonjour a tous !

J'ai un probleme de maths; mais qui a une importance dans une entreprise industrielle:

Je dois calculer la longueur totale d'une spirale,( créée en réalité par une découpe d'une "feuille" de bois d'epaisseur 8mm sur un billon de 43 cm de diametre, qui tourne,(deroulage de bois pour du contre-plaqué) ce qui nous donne donc une spirale dont le "e" de cette page web

http://www.mathcurve.com/courbes2d/archimede/archimede.shtml

est egal a 8 mm

J'arrive donc a une valeur pour "a", et pour trouver "n", j'ai tenté de trouvé le nombre de "tours" la spirale ferait dans mon cas, mais je ne comprends pas car la longueur de cette spirale grace a la formule calculée ainsi n'est pas vraisemblable, (je trouve 2.7 m !! )
Mon professeur de mathematique m'a dit que une longueur de spire de spirale n'etait pas définie, et donc je ne sais pas ce qu'on entend par spire, et donc si je dois faire la somme des spires de Diametre= 0 a Diametre = maximal , ou si la formule marche dans mon cas .
J'espere que vous aurez compris mon probleme, et que vous pourrez m'aider a le résoudre, ce qui m'arrangerait fortement.

Pour info, si vous pouvez m'aider, j'ai trouvé:
e=8mm => a=0.8/2*Pi
n= 430mm/8 = 53.75 "tours"
et donc L=2726.9mm.

Merci beaucoup si quelqu'un peut m'aider

par **alben** » 23 Oct 2007, 20:02

bonjour,
Les solutions les plus simples ont l'avantage d'être plus fiables...
Ton billon a sur surface de coupe de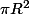

soit en centimètres² 3,14x21.5² = 1542 cm².
La coupe de ta feuille sera de surface Lx0,8 cm²=1542
Donc L =1815 cm =18,15 mètres
Apès on peut épiloguer sur le fait que la découpe fait perdre de la matière, que l'épaisseur n'est pas parfaitement homogène et que le redressement de la feuille va l'allonger...
Mais ce sera pas loin de 18 m et n'importe quel gamin de primaire peut vérifier que ça marche :zen:

par **buggy** » 23 Oct 2007, 20:20

Non car en fait on coupe pas dans le sens du diametre, mais dans la longueur, donc en fait c'est comme si tu fais tourner un cylindre, et que tu a un couteau de la longueur du billon, ( ici 1m ) et qui coupe 8mm de bois et donjc qui fait une bande de bois d'epaisseur de 8mm tres longue, c'est cette longueur que je veux calculer.
Je crois que tu avais mal compris, si c'est moi qui me suis trompé peux tu me reexpliqué ton calcul d'aire, car je ne vois pas pourquoi on s'en interesse ici.
Merci

par **alben** » 23 Oct 2007, 20:27

Ce qui j'avais compris, c'est que ton cylindre était découpé comme un rouleau de PQ. Ce n'est pas ça ?

par **buggy** » 23 Oct 2007, 20:31

oui c'est sa, tout a fait, et la largeur de ta feuille est de 8mm , mais je comprends pas pourquoi tu passe par la surface, en fait c'est la surface du coté du billon, et tu calcule ce que tu enleve ? packe je trouve etrange le resultat ( qui a l'air tout a fait vraissemblable) de la fason dont tu le fait, car dans mon esprit il falai une spirale..

par **alben** » 23 Oct 2007, 20:46

Une fois ta feuille découpée, image que tu l'enroules à nouveau. Tu vas reconstituer ton cylindre et la surface de sa section circulaire sera bien égale à la surface de la tranche de ta feuille étalée (pour mieux voir dis-toi que tu veux dorer la tranche de ta feuille d'un seul coté. Est-ce que tu consommeras plus de peinture si tu la peint avant de la découper ou après ?)

par **buggy** » 23 Oct 2007, 20:48

ah oui d'accord, je te remercie beaucoup, ca m'a beaucoup aidé, pour que tu saches pourquoi je cherchais ca, c'etait pout voir combien je gagne si je passe a 7mm au lieu de 8 mm ! merci encore ! a bientot

Calcul Spirale

Calcul Spirale

Qui est en ligne