Bonjour,
le fil de mon post précédent sest arrêté un peut trop tôt, il me manque léquation de la position du centre du rayon de courbure dune spirale dArchimède de type
ro= a*téta + b
avec rayon de courbure
R = (ro²+ro'²)^3/2 / (ro²+2ro'²-ro*ro'')
Merci à tous et en particulier à Quidam et C pi qui mont bien aidé dans mon post précédent.
Patrick
Centre rayon de courbure d'une spirale d'Archimède
3 messages
- Page 1 sur 1
Bonsoir
avec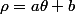 ,
, 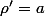 et
et 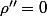
l'expression du rayon de courbure se simplifie quelque peu :
 ^{\frac{3}{2}}}{\rho^{2}+2\rho^{\prime2}-\rho \rho^{\prime\prime}} = \frac{\left(\rho^{2}+a^2\right)^{\frac{3}{2}}}{\rh^2+2a^2})
En ce qui concerne le lieu des centres de courbure de la spirale d'Archimède, c'est la développée dont les équations paramétriques sont données sur cette page.
Pour faciliter l'écriture au clavier, je te propose les notations suivantes :
P(r,t) le point courant de la spirale d'équation polaire r = at+b
ou P(x,y) ce même point de la spirale
dont les coordonnées cartésiennes paramétriques sont
x = r.cos(t) = (at+b).cos(t) et y = r.sin(t) = (at+b).sin(t)
d'où l'on déduit les dérivées premières
x' = a.cos(t)-(at+b).sin(t) et y' = a.sin(t)+(at+b).cos(t)
et les dérivées secondes
x" = -2a.sin(t)-(at+b).cos(t) et y" = 2a.cos(t)-(at+b)sin(t)
Ces éléments permettent de calculer le rapport Q
figurant dans les deux équations paramétriques de la développée
dont le numérateur x'²+y'² se réduit à a²+r²
et dont le dénominateur x'y"-x"y' se ramène à 2a²+r²,
donc Q = (a²+r²)/(2a²+r²) avec r² = x²+y² = (at+b)²
Si l'on désigne par C(g,h) le centre de courbure
correspondant au point P(x,y) de la spirale,
ses coordonnées paramétriques sont
g= x-Q.y' = x-Q.[a.sin(t)+x]
et h = y+Q.x' = y+Q.[a.cos(t)-y]
En calculant PC² = (g-x)²+(h-y)² = Q².(a²+r²)
on retrouve - et c'est rassurant ! - le carré du rayon de courbure
R² = (a²+r²)³/(2a²+r²)²
Dans le cas de la spirale considérée,pmfontaine a écrit:rayon de courbure dune spirale dArchimède de type
ro= a*téta + b
avec rayon de courbure
R = (ro²+ro'²)^3/2 / (ro²+2ro'²-ro*ro'')
avec
l'expression du rayon de courbure se simplifie quelque peu :
En ce qui concerne le lieu des centres de courbure de la spirale d'Archimède, c'est la développée dont les équations paramétriques sont données sur cette page.
Pour faciliter l'écriture au clavier, je te propose les notations suivantes :
P(r,t) le point courant de la spirale d'équation polaire r = at+b
ou P(x,y) ce même point de la spirale
dont les coordonnées cartésiennes paramétriques sont
x = r.cos(t) = (at+b).cos(t) et y = r.sin(t) = (at+b).sin(t)
d'où l'on déduit les dérivées premières
x' = a.cos(t)-(at+b).sin(t) et y' = a.sin(t)+(at+b).cos(t)
et les dérivées secondes
x" = -2a.sin(t)-(at+b).cos(t) et y" = 2a.cos(t)-(at+b)sin(t)
Ces éléments permettent de calculer le rapport Q
figurant dans les deux équations paramétriques de la développée
dont le numérateur x'²+y'² se réduit à a²+r²
et dont le dénominateur x'y"-x"y' se ramène à 2a²+r²,
donc Q = (a²+r²)/(2a²+r²) avec r² = x²+y² = (at+b)²
Si l'on désigne par C(g,h) le centre de courbure
correspondant au point P(x,y) de la spirale,
ses coordonnées paramétriques sont
g= x-Q.y' = x-Q.[a.sin(t)+x]
et h = y+Q.x' = y+Q.[a.cos(t)-y]
En calculant PC² = (g-x)²+(h-y)² = Q².(a²+r²)
on retrouve - et c'est rassurant ! - le carré du rayon de courbure
R² = (a²+r²)³/(2a²+r²)²
Bonjour,
J'ai bien étudier ta réponse et je crois que je devrais m'en sortir.
Merci beaucoup et probablement à bientôt sur ce forum qui est super et très pratique pour des gens comme moi qui aiment les maths (c'est pas une maladie grave ?) mais qui n'ont que rarement l'occasion de les utiliser à ce niveau.
Patrick
J'ai bien étudier ta réponse et je crois que je devrais m'en sortir.
Merci beaucoup et probablement à bientôt sur ce forum qui est super et très pratique pour des gens comme moi qui aiment les maths (c'est pas une maladie grave ?) mais qui n'ont que rarement l'occasion de les utiliser à ce niveau.
Patrick
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 93 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
