Les nombres

[lapras]

Bonsoir,
voila une question me trotte dans la tête depuis quelques temps :
Comment démontrer que le produit de deux nombres de signes négatif est positif ?

Merci d'avance

Lapras

[Flodelarab]

Bonsoir,
voila une question me trotte dans la tête depuis quelques temps :
Comment démontrer que le produit de deux nombres de signes négatif est positif ?

Merci d'avance

Lapras

Qu'est ce que le signe moins ? Qu'est ce qu'un négatif ?


Le signe moins signifie juste "dans l'autre sens".
Pour un nombre, si on change de sens, on passe de l'autre coté du zéro.

Donc si tu change 2 fois de sens, tu reviens dans le sens de départ

C'est aussi bête que ça.

C vrai pour les nombres, les vecteurs, les qualités etc .......

[Joker62]

Soit x et y deux réel négatifs strictement

Alors -x est strictement positif
-y est strictement positif

Le produit de 2 positifs est positifs donc

(-x)(-y) est strictement positif

Donc - (-x)(-y) = x(-y) = (-y)x est strictement négatif

Donc -(-y)x = yx = xy est strictement positif

C'est space hein ?
Maintenant faut admettre que le produit de deux positifs est positif

[Flodelarab]

Soit x et y deux réel négatifs strictement

Alors -x est strictement positif
-y est strictement positif

Le produit de 2 positifs est positifs donc

(-x)(-y) est strictement positif

Donc - (-x)(-y) = x(-y) = (-y)x est strictement négatif

Donc -(-y)x = yx = xy est strictement positif

C'est space hein ?
Maintenant faut admettre que le produit de deux positifs est positif

J'ai pas compris ce qui doit etre spicy .....
Ni ce que ça explique.

[Joker62]

bah j'vais porter plainte contre mon prof d' Analyse de première année lol

[Flodelarab]

Il est censé y avoir une incohérence ?

[lapras]

pas mal la démo joker, mais comme tu le dis, il reste à démontrer que le produit de deux positifs est positif.
Ca semble évident, mais pourquoi ?
Un axiome ?

[Flodelarab]

pas mal la démo joker, mais comme tu le dis, il reste à démontrer que le produit de deux positifs est positif.
Ca semble évident, mais pourquoi ?
Un axiome ?

!!! :doh: Là, j'ai l'impression d'avoir craché en l'air.

Lapras, peux tu me dire ce que tu comprends de la démonstration de Joker ?

Pour moi il applique la définition de l'opérateur unaire "moins" avant de l'avoir défini. Et s'il l'avait défini comme je l'ai défini, alors je ne vois pas l'intérêt de son étude exhaustive de cas.

[nuage]

Salut,
on peut remonter à la définition de :
c'est l'ensemble des classes d'équivalence de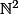 modulo la relation 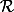définie par ssi 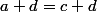. erreur ici
On défini ensuite le produit par .
On montre que cette définition est compatible avec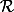 et la règle des signes en découle.

Ps : j'ai enseigné ça en 5°, il y a longtemps.

[modification]
ssi .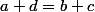
Toutes mes excuses pour cete faute de frappe.

[lapras]

Petit probleme de notation nuage :
(a,b)R(c,d) ???

[nuage]

Salut lapras,
j'ai corrigé une erreur ci-dessus.
Mais je ne suis pas certain de bien comprendre ta remarque.
Qu'est ce qui te gêne dans (a,b)R(c,d) ?

[lapras]

je ne connais juste pas la signification des notations
:triste:

[SimonB]

je ne connais juste pas la signification des notations
:triste:

C'est la définition de la relation R (relation qui relie deux éléments de ton ensemble) : x est relié à y si et seulement si...

Des exemples de relations plus courantes que tu as l'habitude de manipuler, je pense : la relation "inférieur ou égal" sur , la relation d'inclusion sur des ensembles...

[nuage]

(a,b)R(c,d) signifie que les couples (a,b) et (c,d) sont en relation (ici équivalents).
On démontre (ce n'est pas difficile) que R est une relation d'équivalence
cad que si x, y et z sont des éléments de
est toujours vrai

[Joker62]

Ree
Dans mon cour de L1 c'était pas fait exactement pareil
On créer d'abord une partie P et une partie -P tel que leur intersection soit vide

Mais c'est vrai que le moins tapé n'a aucun sens puisque pas définit.

[Miya]

De façon algébrique, il faut revenir aux définitions...
Z muni de l'addition est un anneau commutatif (pas grave si on ne sait pas ce que c'est).
On montre que pour x et y éléments de Z, (x)(-y) = -(xy) (puisque xy + x(-y) = x(y-y) = 0), et de même que (-x)y = -(xy)
Il s'ensuit que (-x)(-y) = -(-(xy)), c'est à dire que c'est l'opposé de -(xy), donc que -(-xy) + (-xy) = 0 = xy + (-xy) -> (-x)(-y) = xy (d'où l'extraordinaire égalité)

C'est simplement revenir à ce que signifie être l'opposé, et bidouiller les formules