Devoir maison sur les variables

[maeva_71]

Voila j'ai un devoir maison mais je ne comprend rien,je suis en premiere ES et j'ai un peu de mal(en realité beaucoup!)en maths.Pourriez vous m'aider a résoudre ce devoir!Merci d'avance!!!!

On considere la fonction f définie sur [-7;7] par f(x)=8x+6/x2+1(ce lis 8x+6 sur x au carré + 1) et Cf sa courbe représentative dans un repere orthonormal du plan.
1°Calculer f '(x).Etudier son signe et en deduire le tableau des variations de la fonction f sur [-7;7].On précisera la valeur des extremums.
2°a)Déterminer les coordonnées des points d'intersection de la courbe Cf avec les axes.
b)Soit D la droite d'équation y=-x+6
Déterminer les coordonnées des points d'intersection de la courbe Cf avec la droite D.
3°a)Déterminer l'équation réduite de la tangente T a Cf au point d'abcisse 0.
b)Dans le repere (o;i;j)(sur i et j il y a une fleche(désolée l'informatique n'est pas mon fort non plus!)),tracer D,T,les tangentes horizontales,puis la courbe Cf.
D'apres le graphique,la tangente T coupe-t-elle la courbe Cf?Si oui en quel(s) point(s)?

Si vous n'arrivez pas a m'expliquer tout le dm a cause des graphiques par exemple il serait sympa juste de m'aider a la premiere question pour me mettre au moins sur la voie!Bonne chance!!!!

[fonfon]

salut,

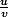
tu n'arrives pas à calculer la dérivée pourtant f est de la forme de dérivée

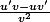
[maeva_71]

ah donc u=8x+6 et u '=8 quand a v = x2+1 et v '=3x+1.
ENfin si je ne me trompe pas!

[fonfon]

ah donc u=8x+6 et u '=8

presque car il faut ecrire u(x)=8x+6 donc u'(x)=8

quand a v = x2+1 et v '=3x+1.

non, c'est faux v(x)=x²+1 donc v'(x)=2x

j'ai changé ma faute

[maeva_71]

merci cela m'aide beaucoup,j'ai deja le point de départ de mon devoir!merci beaucoup!!!!

[fonfon]

tu peux ecrire ce que tu trouves pour f'(x) si tu veux que je te dise si tu as bon ou faux c'est comme tu veux

[maeva_71]

Je trouve f '(x)=8xau carré-16x+20 sur (x au caré + 1)au carré.
Mais les carrés ne s'annule-t-il pas?

[fonfon]

Je trouve f '(x)=8xau carré-16x+20 sur (x au caré + 1)au carré.
Mais les carrés ne s'annule-t-il pas?

tu as fait une erreur quelque part









j'ai factorisé ( utiliser le discriminant pour -2x^2-3x+2) au maximum afin d'étudier le signe de la dérivée

[maeva_71]

Pourquoi x2x?v ' (x) est bien égale a 2,pas 2x,non?

[fonfon]

excuse moi j'ai fait une faute de frappe c'est v'(x)=2x désolé

[maeva_71]

ah d'accord bah merci alors...j'aurais jamais pu faire cela moi meme!

[fonfon]

essaie de continuer si tu as des problèmes n'hésite pas

Bon courage