Calcul d'un angle

[mitomat]

Bonjour, pour un projet de programmation C++ en visualisation, j'ai un problème de géométrie.

Voilà mon problème :
_ un cercle de centre C(0,0) et de rayon r=3.
_ un point a de coordonnées x=0, y=3
_ un second cercle de centre C(0,0) et de rayon r=6.

je souhaite disposer 4 points sur le second cercle, à proximité du point a, sachant que ces 4 points sont à distances égales et qu'ils sont disposés selon un angle de PI/2 autour de a. J'aimerais savoir comment calculer les coordonnées de ces 4 points.

J'espère m'être fait comprendre, je joindrais un schéma sinon
Merci

[mitomat]

[nuage]

Salut,
pour le premier point marqué sur ton schéma (dans le sens trigonométrique).
Ses coordonnées sont solutions de
et
Son abscisse est la solution positive de .
Après il est facile de calculer les angles.

[mitomat]

Merci, de ta réponse, mais je m'aperçois que j'aurais principalement besoin de calculer l'angle entre le point le plus à gauche, celui le plus à droite, et le centre C. (sachant que l'angle à partir de A entre ces 2 points est de PI/2)

[nuage]

A partir de ma réponse précédente, et à vu de nez, je dirais que cet angle est

[mitomat]

Oui mais j'ai besoin de l'implémenter dans un programme, donc j'aurais besoin d'avoir la méthodologie précise à partir des données dont je disposes :p

[fahr451]

bonsoir

les programmes sont à l'étage en dessous ici c 'est tout manuel

[nuage]

Plus précisément :
avec les équation que je t'ai donné on trouve les coordonnées du point "le plus à droite" disons M

L'angle que tu cherche est deux fois l'angle .
Son cosinus est .
D'où le résultat.

A+

[nuage]

Disons une formule générale :
Soit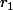 le rayon du petit cercle et 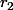celui du grand cercle.
la droite AM a pour équation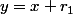 et le grand cercle . De plus on sait que l'abscisse de M, notée 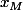est positive.
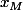est la solution positive de
donc

et

On a donc

Voila.
les calculs sont justes mais je ne suis pas sûr de ne pas avoir fait de fautes de frappe.

A+

[edit] j'en ai corrigé mais il en reste peut-être

[mitomat]

Disons une formule générale :
Soit le rayon du petit cercle et celui du grand cercle.
la droite AM a pour équation et le grand cercle . De plus on sait que l'abscisse de M, notée est positive.
est la solution positive de
donc

et

On a donc

Voila.
les calculs sont justes mais je ne suis pas sûr de ne pas avoir fait de fautes de frappe.

A+

[edit] j'en ai corrigé mais il en reste peut-être

merci j'vais regarder ça