Résolution d'équations

[loudakota]

Bonjour,
j'ai repris cette année des études mais mes souvenirs de maths du lycée sont bien trop loin pour cet exercice si quelqu'un voulait bien m'aider.
On considere la fonction, f définie sur]o;+&[ par:
f(x) = 1/(1+x2)

a) résoudre, pour y réel donné, y €]o;1], l'équation (d'inconnue x) f(x)=y, (on comptera le nombre de solutions dans [à,+1[).
b) en déduire que f est une bijection de [0;+&[ sur]0;1].

Désolé, j'ai pas trouvé le signe pour infini ni pour appartient ni même pour mettre x au carré. J'espere quand même être lisible.
Merci pour votre aide.

[mathelot]

on rmarque que pour 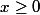, ie,



Il est donc naturel de se donner un nombre y dans ]0;1]
et de chercher son ou ses antécedents dans
pour ce faire, on résoud l'équation d'inconnue x:
f(x)=y
soit



comme
il existe deux nombres x qui conviennent:
et
si on se restreint à choisir x dans
la fonction
donne l'antécédent de y. C'est donc la fonction réciproque de f, notée .
f et sont deux bijections réciproques. Le domaine de définition de l'une est l'ensemble d'arrivée de l'autre.


Cordialement,

Bonne nuit. :dodo:

[loudakota]

Merci beaucoup pour ton aide. Maintenant que tu me le dis cela me parait clair.