Vecteurs

[Tysse]

Bonjour !
J'ai un dm à faire sur les vecteurs sauf que j'y arrive pas ...
Déjà que j'ai du mal avec les vecteurs en général...
Alors je viens demander de l'aide

On considère un tétraèdre abcd.
On note I,J, K et L les milieux respectifs des segments [AB][BC][CD][AD]. On note également le point G milieu de [IK] et le point Y définie par vecteurYB=2/3vecteurKB

La premiere question que j'ai réussie était démontrer que vecteurAC+ vecteurAD=2vecteursAK

Mais la deuxième j'y arrive pas ..
Il faut déduire que vecteurAB+vecteurAC+vecteurAD=4vecteursAG

Donc si quelqu'un pouvait m'aider se serait super !
Merci d'avance

[Ben314]

Salut,
Le terme de gauche de l'égalité ne contient que des points "de base" (donnés au début de l'énoncé) alors qu'à droite tu as le point G qui est construit dans l'énoncé. Donc le plus naturel, c'est de partir du terme de droite et d'utiliser la définition de G pour l'enlever de l'expression. Et comme G est défini comme le milieu de [IK], il faut faire apparaître (via la relation de Chasle) par exemple le vecteur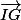 (ou ) pour pouvoir dire qu'il est égal à (ou ). En procédant de la sorte, tu n'aura plus de point G, mais tu aura à la place les points I et K et rebelote : tu te débrouille avec Chasles pour faire apparaître par exemple 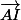et de façon à pouvoir dire qu'ils sont égaux à et . Et là, tu n'aura plus que les points de bases dans ton expression et il suffira éventuellement de réutiliser une ou deux fois Chasles pour trouver le résultat demandé.

[catamat]

Bonjour

Une autre possibilité est d'utiliser la question précédente

Remplacer par

et par car I est milieu de [AB]

après simplification par 2 on obtient une égalité pas bien difficile à démontrer

[Tysse]

Merci beaucoup ! J'ai eu du mal mais j'ai réussi à finir !
Et j'ai une autre question,
Après il faut que je démontre que les points A, G et Y sont alignés.
J'ai tenté de calculer AG et AY pour voir si je trouvais pareil sauf que je trouve pas la même chose ...

Je trouve AB+1/2DC+2/3CB pour le vecteur AY
Et je trouve AB+ 2/3DC+1/3CB+CG pour le vecteur AG..

[catamat]

Pour cette question il faut là aussi se servir des questions précédentes...

On connait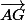 en fonction de , et .

Donc il faut exprimer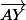 en fonction des trois mêmes vecteurs, on trouvera que ce vecteur est colinéaire à 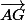c'est à dire de la forme où k est un réel à déterminer.