Équation de cercle et paramètre

[Alexiiiiiiiii]

Bonjour je n’arrive pas à résoudre cet exercice. Est ce que vous pourriez m’aider.

Soit m un nombre réel. On considère l’ensemble des points M(x;y) vérifiant l’équation: x²-2m+y²-8my+16m²+6m-9=0
1) Montrer que cette équation est celle d’un cercle dont on déterminera le centre Ω et le rayon r.
2) déterminer l’ensemble décrit par Ω lorsque m décrit ℝ.
3) est-il possible de trouver une valeur de m telle que Ω appartienne à la droite d’équation 3x-5y+36=0?

[vam]

Bonjour
tu n'aurais pas oublié un x en recopiant ?

[Alexiiiiiiiii]

Bonjour
Oui pardon vous avez raison c’est -2mx.
Mais avez vous compris l’exercice ?

[vam]

ben oui...tu as vu un peu le même principe avec les équations du seconde degré et la mise sous forme canonique

x²-2mx+y²-8my+16m²+6m-9=0

x²-2mx est le début d'un carré

(x-m)²=x²-2mx+4m²
donc tu peux remplacer x²-2mx par (x-m)²-4m²

ensuite tu fais de même avec y²-8my

et

tu vas arriver à une expression du genre


tu essaies ?

[Alexiiiiiiiii]

Je ne comprend pas. Ce que vous m’avez expliqué c’est pour la 1 ère question. ( d’ailleurs jài fait une autre erreur dans l’énoncé c’est -9 )
Moi pour la première question j’ai trouvé comme résultat à la fin : (x-m)²+(y-4m)²=m² + √6m-3

Mais je ne comprend pas ce qui est demandé aux deux questions suivantes

[vam]

( d’ailleurs jài fait une autre erreur dans l’énoncé c’est -9 )

où ?
peux-tu réécrire cette équation correctement, parce que là, ...
ben oui c'est pour la question 1, indispensable avant de pouvoir faire les suivantes

[Alexiiiiiiiii]

L’équation de l’énoncé c’est: x²-2mx+y²-8my+16m²+6m-9=0

Mais je ne comprend pas ce qui est demandé pour les deux autres questions

[vam]

Je ne suis pas d'accord avec ce que tu trouves dans ton second membre ici

(x-m)²+(y-4m)²=m² + √6m-3

donc à revoir
2) à lire cette équation de cercle, tu connais les coordonnées du centre.

si m décrit R, où se baladent des points ?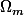

3) impose le fait que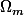 appartienne à cette droite, et tu vas trouver m (ou pas)

[Alexiiiiiiiii]

D’accord merci beaucoup