Combinaisons

[Grandpere13]

Un jeu pour les tous petits comporte des cartes sur lesquels figurent 6 animaux différents.
Deux cartes quelconques ont en commun un animal et un seul.
J'ai essayé de trouver une relation entre le nombre d'animaux par carte, le nombre total d'animaux et le nombre de cartes.
L'expérience menée de 2 à 5 animaux par carte montre que pour "n" animal par carte le nombre total d'animaux doit être de N= 1+n(n-1) et que le nombre de cartes est égal à ce nombre N, chaque animal figurant dans n cartes différentes :
N = 3 pour 2 animaux par carte ; 7 pour 3 ; 13 pour 4 ; 21 pour 5.
L'expérience pour des nombres plus élevés devient difficile !!!!
J'ai essayé de démontrer cela d'une manière générale :
Si l'on prend une carte quelconque de n animaux, les autres cartes qui contiennent l'un d'eux doivent avoir n-1 autres animaux tous différents. Le nombre total d'animaux, ainsi que le nombre de cartes parait donc bien être N =1 + n(n-1) ; chaque animal se retrouvant ainsi dans n cartes différentes.
Ensuite, je bloque :
- Y a-t'il une solution pour toutes les valeurs de n ?
- Si oui, quelle est la méthode pour définir l'ensemble des combinaisons ?

[lyceen95]

Je remets tout l'énoncé dans l'ordre ...

On a animaux différents.
Sur chaque carte, il y a animaux.
Chaque animal doit apparaître exactement fois.
Si je prends 2 cartes, il doit y avoir au maximum un animal en commun.
Si je prends 2 animaux différents, il doit y avoir une carte (et une seule) qui contient ces 2 animaux.

Donc effectivement, si on a animaux par carte, l'animal n°1 sera associé à autres animaux sur chacune des cartes où il apparaît.
Il doit donc y avoir animaux autres que l'animal n°1.
Et donc animaux en tout.
Et comme chaque animal apparaît fois , et qu'on a animaux sur chaque carte, le nombre de cartes est égal au nombre d'animaux.
= nombre de cartes =nombre d'animaux =

Y-a-t-il systématiquement une disposition qui va marcher ?
Je pense que oui, mais aucune certitude.
On va essayer pour n=7, avec méthode. 1+n(n-1)=43 donc 43 cartes.
on va donc prendre les 26 lettres de l'alphabet majuscules + 17 minuscules.

Code: Tout sélectionner

ABCDEFG
AHIJKLM
ANOPQRS
ATUVWXY
AZabcde
Afghijk
Almnopq
BHNTZfl
BIOUagm
BJPVbhn
BKQWcio
BLRXdjp
BMSYekq
CHOVcjq
CIPWdkl
CJQXefm

Je te laisse continuer, mais ça a l'air de fonctionner.

J'avais vu un article sur un site type CNRS ( il y a un site de vulgarisation avec des trucs relativement amusants) sur un jeu un peu similaire.
Mais ce n'était pas le même jeu que toi, c'est sûr.
Peut-être qu'en faisant quelques recherches avec le nom du jeu, tu trouveras quelque chose.

[GaBuZoMeu]

Bonsoir,

Il y a une interprétation géométrique qui peut être intéressante : les cartes sont les droites du plan projectif sur un corps fini, les animaux sont les points du plan.
Sur un corps à q éléments, les droite projectives ont q+1 points, et le plan a q^2+q+1 points.

Avec n = q+1, le nombre de points du plan (d'animaux) est bien n(n-1)+1.
Cette interprétation géométrique ne marche que si q est une puissance de premier (2,3,4,5,7,8,9,11,13 ...)

[Grandpere13]

Merci de vos contributions.
Pour mes essais de n=2 à 6, j'ai utilisé des matrices en croisant animaux et cartes.
Cela marche de 2 à 5 mais pour 6 je n'y suis pas parvenu.
Il faut dire qu'au delà du rang n des lignes et colonnes cela devient très fastidieux.
J'aurais bien montré les matrices mais je me heurte à "extension interdite"
La notion de "puissance de premier" parait intéressante car cela pourrait expliquer le problème du 6.
Malheureusement j'ignore totalement la notion de "plan projectif", je vais faire des recherches !
Pour ma défense, je dois dire que mon dernier cours de math date des années 60...

[GaBuZoMeu]

Bonjour,

Pour n=7, ça ne va pas marcher : 7=6+1, et il n'y a pas de plan projectif d'ordre 6.

Pour n=6, il y a bien un plan projectif d'ordre 5 qui a 31 points et 31 droites. C'est le plan projectif sur le corps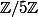 . Je noterai 0,1,2,3,4 les éléments de ce corps (les entiers modulo 5).
Les points (animaux) sont :
- les 25 points du plan affine : les (x,y) où x et y sont des éléments de {0.1.2.3.4},
- les 6 points de la droite de l'infini qu'on peut noter par les pentes de leur direction : 0,1,2,3,4,.

À part la droite de l'infini, les droites sont les 25 droites d'équation y=ax+b (avec le point à l'infini correspondant à la pente a) pour a,b dans {0.1.2.3.4}, et les 5 droites verticales x=c (avec le point à l'infini ) pour c dans {0.1.2.3,4}. Ça fait bien également 31 droites (cartes).