Exo sur les séries niveau licence 2
15 messages
- Page 1 sur 1
exo sur les séries niveau licence 2
bonjour, j'ai besoin d'un petit peu d'aide pour un exo d'analyse.
on me demande Étudier la nature de la série de terme général : u_{n}
avec u_{n}=n^{\alpha } \int_{0}^{\frac{\pi }{n}}{sin^{\beta }(x)}dx avec alpha dans IR et beta strictement plus grand que 0
j'ai fais la convergence absolue mais pour le reste je sais pas
on me demande Étudier la nature de la série de terme général : u_{n}
avec u_{n}=n^{\alpha } \int_{0}^{\frac{\pi }{n}}{sin^{\beta }(x)}dx avec alpha dans IR et beta strictement plus grand que 0
j'ai fais la convergence absolue mais pour le reste je sais pas
Re: exo sur les séries niveau licence 2
Que trouvez-vous déjà comme condition d'absolue convergence?
Modifié en dernier par issoram le 27 Déc 2020, 21:42, modifié 1 fois.
Re: exo sur les séries niveau licence 2
alpha <0, ducoup j'ai essayer de trouver pour alpha =0 en fonction de betamais j'arrive pas
Re: exo sur les séries niveau licence 2
Comment arrivez-vous à ce résultat?
Modifié en dernier par issoram le 27 Déc 2020, 22:08, modifié 1 fois.
Re: exo sur les séries niveau licence 2
je prend la valeur absolue de u_n puis je majore la valeur absolue de l'intégrale par l'intégrale de la valeur absolue, enfin je majore sin ^b(x) par 1 et l'intégrale de 0 à pi/n de 1 c'est la longeur de l'intervalle ainsi j'ai |u_n|=n^alpha*pi/n ducoup absolument convergent pour alpha<0 maisapres avoir fais ca je suis perdu
Re: exo sur les séries niveau licence 2
Bonjour
Je n'ai vraiment pas le temps de développer mais :
il s'agit d'une série à termes positifs pour n>2 et donc le critère de comparaison est applicable
(en outre on a observé un "faux problème" de convergence en 0, sachant bêta>0)
nous avons pour n>2 :
0<Pi/n<Pi/2
alors sur ]0,Pi/n]
(2/Pi)x<sin(x)<x
ceci devrait permettre d'utiliser le critère de comparaison
Bon courage
Je n'ai vraiment pas le temps de développer mais :
il s'agit d'une série à termes positifs pour n>2 et donc le critère de comparaison est applicable
(en outre on a observé un "faux problème" de convergence en 0, sachant bêta>0)
nous avons pour n>2 :
0<Pi/n<Pi/2
alors sur ]0,Pi/n]
(2/Pi)x<sin(x)<x
ceci devrait permettre d'utiliser le critère de comparaison
Bon courage
Re: exo sur les séries niveau licence 2
petit update: ainsi grâce à vous, j'ai réussi a majoré le reste au rang 2par 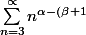}\frac{\pi ^{\beta +1}}{\beta +1}}) qui est équivalent (car >0) à
qui est équivalent (car >0) à 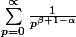 convergent pour
convergent pour  .
.
Ducoup, ma conclusion que c'était absolument convergent pour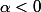 est fausse ?
est fausse ?
Ducoup, ma conclusion que c'était absolument convergent pour
Re: exo sur les séries niveau licence 2
Bonjour,
quelques petites remarques d'abord :
- La série est à termes positifs : la convergence absolue c'est la convergence
-Évitez le mot "équivalent", qui a un sens bien précis, lorsque vous voulez dire en fait :
ces deux séries sont de même nature.
Ensuite (je note a pour alpha et b pour bêta)
si a<0 alors
-a>0 et donc
b+1-a>b+1>1 (sachant b>0) convergence
plus généralement, pour bien mener la discussion :
observez la double inégalité que je vous ai indiquée :
à une constante multiplicative près, vous retrouvez la même série coté minoration et coté majoration
(c'est celle que vous avez citée)
or une constante multiplicative est sans importance pour la nature d'une série...
La discussion va donc se mener à partir des valeurs de b+1-a
Bon courage
quelques petites remarques d'abord :
- La série est à termes positifs : la convergence absolue c'est la convergence
-Évitez le mot "équivalent", qui a un sens bien précis, lorsque vous voulez dire en fait :
ces deux séries sont de même nature.
Ensuite (je note a pour alpha et b pour bêta)
si a<0 alors
-a>0 et donc
b+1-a>b+1>1 (sachant b>0) convergence
plus généralement, pour bien mener la discussion :
observez la double inégalité que je vous ai indiquée :
à une constante multiplicative près, vous retrouvez la même série coté minoration et coté majoration
(c'est celle que vous avez citée)
or une constante multiplicative est sans importance pour la nature d'une série...
La discussion va donc se mener à partir des valeurs de b+1-a
Bon courage
Re: exo sur les séries niveau licence 2
merci beaucoup de votre aide c'est super sympa, passez de bonne fetes.
15 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 49 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :


