Bonjour,
J'ai un exercice que je n'arrive pas à résoudre:
| 3-m -2 3 |
On pose la matrice M=A-mI=| 1 -m 2 |
| 0 0 2-m |
1) Calculer le déterminant de la matrice M. Pour quelles valeurs de m, la matrice M est-elle inversible?
2) Démontrer que Ker (f - Id) et Ker (f-2Id) sont des droites vectorielles dirigées respectivement par des vecteurs u1 et u2 ( On prendra u1 et u2 avec 1 pour 2ème composante).
3) Déterminer le vecteur u3, avec 1 pour 2ème composante, tel que f(u3) = u2+2u3.
4) Démonter que B' = (u1,u2,u3) est une base de R3.
5) Déduire des questions 2 et 3 la matrice A' de f dans la base B'.
J'ai reussi les 2 premières questions mais je ne vois pas du tout comment faire la suite
Merci d'avance pour vos réponses.
Exercice sur les matrices
8 messages
- Page 1 sur 1
Re: exercice sur les matrices
Tu ne le dis pas, mais je suppose que  est la matrice de
est la matrice de  (dans la base canonique de
(dans la base canonique de 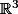 ).
).
Tu connais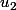 . Alors
. Alors =u_2+2u_3) est juste un système de trois équations linéaires à trois inconnues (les composantes de
est juste un système de trois équations linéaires à trois inconnues (les composantes de 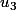 ). Tu devrais savoir le résoudre. Il y a une infinité de solutions, mais on t'impose la deuxième composante.
). Tu devrais savoir le résoudre. Il y a une infinité de solutions, mais on t'impose la deuxième composante.
Tu connais
Re: exercice sur les matrices
Merci beaucoup,
Oui, a est bien la matrice de f.
Je ne vois par contre pas comment poser le système d'équations pour la suite.
Oui, a est bien la matrice de f.
Je ne vois par contre pas comment poser le système d'équations pour la suite.
Re: exercice sur les matrices
Tu as la matrice de  .
.
Tu as les composantes de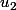
Tu cherches
Vraiment, tu ne vois pas comment traduire=u_2+2u_3) par un système d'équations linéaires en
par un système d'équations linéaires en 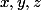 ???
???
Tu as les composantes de
Tu cherches
Vraiment, tu ne vois pas comment traduire
Re: exercice sur les matrices
Je n'ai pas fait les calculs, je te laisse la responsabilité de la correction. Tu peux vérifier que tu as bien =u_2+2u_3) .
.
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 24 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
