Séries de Riemann

par **JésugnonADJAKIDJE** » 23 Avr 2020, 18:50

Salut!
Aidez-moi, svp, à calculer

et

.
Merci!

par **phyelec** » 23 Avr 2020, 21:53

Bonjour,

vous pouvez y arriver en utilisant un développement en série de Fourier de la fonction f

périodique qui vaut x sur

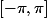
pour la première et Parseval à partir de la première pour en déduire la seconde.

par **JésugnonADJAKIDJE** » 24 Avr 2020, 09:50

Merci, j'arrive à calculer la première. C'est comment déduire la seconde mon problème maintenant.

par **phyelec** » 24 Avr 2020, 17:03

Bonjour,

La formule de Parseval également sur la même fonction fait intervenir les coefficients (que vous avez calculé) a0, an et bn de Fourier au carré et donc vous pouvez en déduire le second résultat.

par **JésugnonADJAKIDJE** » 25 Avr 2020, 00:33

phyelec a écrit:Bonjour,

La formule de Parseval également sur la même fonction fait intervenir les coefficients (que vous avez calculé) a0, an et bn de Fourier au carré et donc vous pouvez en déduire le second résultat.

Merci bien, j'y suis arrivé.

Séries de Riemann

Séries de Riemann

Re: Séries de Riemann

Re: Séries de Riemann

Re: Séries de Riemann

Re: Séries de Riemann

Qui est en ligne