Permutations de Sn
16 messages
- Page 1 sur 1
permutations de Sn
Bonjour
je n'arrive pas à répondre à cette question:
Trouver deux permutations de Sn toutes les deux d'ordre 2 dont le produit est d'ordre n.
Merci bcp.
je n'arrive pas à répondre à cette question:
Trouver deux permutations de Sn toutes les deux d'ordre 2 dont le produit est d'ordre n.
Merci bcp.
Re: permutations de Sn
Bonjour,
tu peux chercher ces permutations dans le groupe diédral Dn (sous groupe de Sn correspondant aux permutations des n sommets d'un polygone régulier par rotations et symétries axiales).
tu peux chercher ces permutations dans le groupe diédral Dn (sous groupe de Sn correspondant aux permutations des n sommets d'un polygone régulier par rotations et symétries axiales).
Re: permutations de Sn
Rebonjour,
malheureusement je n'arrive pas à voir, je prends une symétrie axiale , mais quelle rotation?
malheureusement je n'arrive pas à voir, je prends une symétrie axiale , mais quelle rotation?
Re: permutations de Sn
Peut être la composée de deux symétries axiales bien choisies? Connais tu un élément de Dn d'ordre n ?
Re: permutations de Sn
Autre piste : partir d'une rotation d'ordre n et la composer avec une symétrie axiale pour obtenir une autre symétrie, puis remettre les choses dans l'ordre.
Re: permutations de Sn
Sans passer par le groupe diédral, on peut constater que le produit (que ce soit à gauche ou à droite) d'un cycle de longueur k avec une transposition entre un élément du support du cycle et un élément qui n'est pas dans le support du cycle fournit un cycle de longueur k+1.
&&\\ (12)&&(23)\\ (34)(12)&&(23)\\ (34)(12)&&(23)(45)\\ \vdots\qquad&&\qquad\vdots \end{array})
Re: permutations de Sn
Petite question supplémentaire : soit 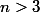 . Montrer que tout élément de
. Montrer que tout élément de  est produit de deux éléments de
est produit de deux éléments de  d'ordre deux.
d'ordre deux.
Re: permutations de Sn
Avec Dn , si les axes de symétries ont un angle de k(2pi/n) , alors leur composée est une rotation d'angle 2k(2pi/n) . Si n est pair 2k n'est pas premier avec n , et la rotation ne sera jamais d'ordre n .
Re: permutations de Sn
Tournesol, deux axes de symétries "successifs" ont un angle (orienté de droites) de 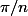 (pense à un carré !) et la composition des symétries est bien une rotation de
(pense à un carré !) et la composition des symétries est bien une rotation de 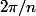
Re: permutations de Sn
@tournesol : pour n=4, l'angle formé entre une médiane et une diagonale dans un carré est pi/4, qui n'est pas un multiple de 2pi/4 = pi/2. Il me semble que tu oublies la moitié des axes.
D'autre part, le groupe diédral est formellement engendré par deux éléments s d'ordre n et t d'ordre 2 tels que tst = s^{-1}. En posant r = st on a alors r² = stst = ss^{-1} = 1 et s = rt.
D'autre part, le groupe diédral est formellement engendré par deux éléments s d'ordre n et t d'ordre 2 tels que tst = s^{-1}. En posant r = st on a alors r² = stst = ss^{-1} = 1 et s = rt.
Re: permutations de Sn
Au temps pour moi . J'ai bien oublié la moitié des axes, aussi bien pour n pair que pour n impair .
Merci à vous deux .
Merci à vous deux .
Re: permutations de Sn
GaBuZoMeu a écrit:Tournesol, deux axes de symétries "successifs" ont un angle (orienté de droites) de(pense à un carré !) et la composition des symétries est bien une rotation de
C'était l'exemple que j'avais en tête!
Re: permutations de Sn
Salut
Comme les supports des différents cycles sont disjoints, quand on regroupe les "symétries axiales", ça reste d'ordre 2.
Une question sans doute plus compliquée, c'est de savoir, pour une permutation donnée, combien il y a de décomposition en produit de deux éléments d'ordre 2.
Une méthode possible est de décomposer la permutation en cycle disjoint puis, pour chaque cycle [d'ordre k] de le décomposer en produit de la même façon qu'on décompose une rotation d'angle 2.pi/k [donc d'ordre k] à l'aide de deux symétries axiales.GaBuZoMeu a écrit:Petite question supplémentaire : soit. Montrer que tout élément de
est produit de deux éléments de
d'ordre deux.
Comme les supports des différents cycles sont disjoints, quand on regroupe les "symétries axiales", ça reste d'ordre 2.
Une question sans doute plus compliquée, c'est de savoir, pour une permutation donnée, combien il y a de décomposition en produit de deux éléments d'ordre 2.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: permutations de Sn
Oui, c'était bien l'idée de décomposer chaque cycle dans la décomposition en produit de cycles disjoints.
Pourquoi n>3 ?
Pourquoi n>3 ?
Re: permutations de Sn
Du fait que, si n=2, lorsqu'on décompose une rotation d'angle pi en produit de deux réflexions une des deux réflexion agit trivialement sur les deux sommets du polygone (à 2 cotés) donc vue comme une permutation des sommets c'est l'identité et elle est d'ordre 1 et pas 2. Bref, dans S2 il n'y a pas moyen d'écrire (12) comme produit de deux permutations d'ordre 2. Idem dans S3. Par contre à partir de S4 on peut écrire (12) comme composée de (12)(34) et de (34) qui sont bien tout les deux d'ordre 2.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
16 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 54 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
