Caractérisation des matrices de permutations
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
ffpower
- Membre Complexe
- Messages: 2542
- Enregistré le: 13 Déc 2007, 04:25
-
 par ffpower » 30 Mai 2009, 16:49
par ffpower » 30 Mai 2009, 16:49
Petit exercice amusant d algebre linéaire:
Soit A une matrice de GL_n(Z), a coefficients positifs, telle que la suite (A^n) soit bornée.Montrer que A est une matrice de permutation
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 30 Mai 2009, 18:03
par yos » 30 Mai 2009, 18:03
Une partie bornée de Gln(Z) est finie donc A est d'ordre fini dans ce groupe.
-
ffpower
- Membre Complexe
- Messages: 2542
- Enregistré le: 13 Déc 2007, 04:25
-
 par ffpower » 30 Mai 2009, 18:29
par ffpower » 30 Mai 2009, 18:29
eact(mais ca ne conclut pas l exercice)
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 30 Mai 2009, 19:10
par yos » 30 Mai 2009, 19:10
Je vois bien que c'est pas fini.
Suite des idées : A est diagonalisable (dans Q par exemple). Ses vp ne pouvant alors être que 1 et -1. Les 1 dominent because la trace.
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 30 Mai 2009, 20:04
par yos » 30 Mai 2009, 20:04
J'ai dit une bétise.

est pas scindé sur Q. La diagonalisabilité dans C est pas intéressante.
-
sniperamine
- Membre Relatif
- Messages: 366
- Enregistré le: 19 Jan 2009, 03:46
-
 par sniperamine » 30 Mai 2009, 20:26
par sniperamine » 30 Mai 2009, 20:26
yos a écrit:J'ai dit une bétise.

est pas scindé sur Q. La diagonalisabilité dans C est pas intéressante.
yos je crois que c'est la trigonalisation qui n'est pas intéressante yos :happy2: car toute matrice dans C est trigonalisable
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 30 Mai 2009, 21:01
par yos » 30 Mai 2009, 21:01
Celle-là est diagonalisable dans C (à valeurs propres racines de 1). Mais ça m'a pas l'air très utile.
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 30 Mai 2009, 22:05
par Nightmare » 30 Mai 2009, 22:05
Salut à tous :happy3:
ffpower, désolé de mon manque de culture mais qu'appelles-tu "matrice de permutation" ? Est-ce simplement une matrice représentant un endomorphisme bijectif de N?
-
sniperamine
- Membre Relatif
- Messages: 366
- Enregistré le: 19 Jan 2009, 03:46
-
 par sniperamine » 30 Mai 2009, 22:25
par sniperamine » 30 Mai 2009, 22:25
yos a écrit:Celle-là est diagonalisable dans C (à valeurs propres racines de 1). Mais ça m'a pas l'air très utile.
ah ok Yos c'est bon je comprends mieux maintenant
-
SimonB
 par SimonB » 30 Mai 2009, 22:58
par SimonB » 30 Mai 2009, 22:58
Nightmare a écrit:Est-ce simplement une matrice représentant un endomorphisme bijectif de N?
C'est une matrice représentant une permutation de {1,...,n}.
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 30 Mai 2009, 23:23
par Doraki » 30 Mai 2009, 23:23
Il me semble que quand on sait que M est diagonalisable dans C on a déjà presque fini.
(A la reflexion, en fait nan c'est pas aussi simple, c'est dur d'utiliser l'hypothèse que les coefficients sont positifs).
Sinon on peut aussi faire un truc plus combinatoire c'est pas très dur mais ça ressemble moins à de l'algèbre linéaire.
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 01 Juin 2009, 06:19
par yos » 01 Juin 2009, 06:19
Doraki a écrit:Il me semble que quand on sait que M est diagonalisable dans C on a déjà presque fini.
J'ai pensé à ça :
Si (e_i) est la base canonique de R^n,
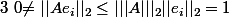
,
la norme subordonnée à la norme euclidienne étant le rayon spectral.
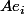
ne peut contenir qu'un 1 et des 0 dans ses coordonnées :
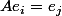
.
L'inversibilité de A assure alors que A permute les
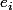
.
-
ffpower
- Membre Complexe
- Messages: 2542
- Enregistré le: 13 Déc 2007, 04:25
-
 par ffpower » 01 Juin 2009, 07:49
par ffpower » 01 Juin 2009, 07:49
Salut :we:
Pourquoi

?
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 01 Juin 2009, 08:05
par yos » 01 Juin 2009, 08:05
Les vp sont des racines de 1 et la norme est le sup des modules des vp.
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 01 Juin 2009, 08:36
par Doraki » 01 Juin 2009, 08:36
Comment tu montres que A est diagonalisable ?
Et puis la norme de A est pas forcément la même que celle de la diagonalisation de A.
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 01 Juin 2009, 08:48
par yos » 01 Juin 2009, 08:48
Elle est diagonalisable car annulée par un polynôme x^k-1.
La norme est pas constante sur les classes de similitude mais les valeurs propres si.
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 01 Juin 2009, 08:57
par Doraki » 01 Juin 2009, 08:57
Ok pour la diagonalisabilité.
En prenant A =
(0 -1)
(1 -1)
T'es en train de dire que sqrt(2) = || A e2 || <= 1 ?
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 01 Juin 2009, 10:16
par yos » 01 Juin 2009, 10:16
En effet : ce doit être le rayon spectral de
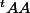
qu'il faut prendre; D'où mon erreur.
Je regarderai plus tard si j'arrive à récupérer le coup.
-
ffpower
- Membre Complexe
- Messages: 2542
- Enregistré le: 13 Déc 2007, 04:25
-
 par ffpower » 29 Juil 2009, 18:41
par ffpower » 29 Juil 2009, 18:41
Petit up avant de donner la solution(c est en fait pas tres dur,et ma solution n utilise rien d algebre linéaire-ca doit etre la meme que doraki)
-
skilveg
- Membre Relatif
- Messages: 462
- Enregistré le: 21 Mai 2008, 21:29
-
 par skilveg » 29 Juil 2009, 20:52
par skilveg » 29 Juil 2009, 20:52
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 64 invités
