Domaine de définition d’une fonction

[Azzedine93]

Bonjour,
J’ai un petit problème dans un exercice:
On me demande de déterminer l’ensemble de définition de la fonction rationnelle puis déterminer l’es limite si aux bornes de leur ensemble

Voici la fonction :

K(x)=(3x-5)+(2+(x+2))

Dans la correction , on me dit que le domaine de définition est : R-{-2} et je ne comprend pas car lorsque x=-2 k(x)=-11.

Merci d’avance

[Sa Majesté]

Voici la fonction :

K(x)=(3x-5)+(2+(x+2))

Bonjour,
Ce n'est pas une fonction rationnelle.

[Azzedine93]

Qu’est ce qu’une fonction rationnelle et irrationnelle ?

[Azzedine93]

Du coup ici c’est 2/(x+2) la fonction rationnelle?

[Sa Majesté]

Oui mais moi je vois 2+(x+2)
Ou alors "c'est mes yeux"

[Azzedine93]

Ah oui désolé je rectifie :

(3x-5)+(2/(x+2)) c’est la fonction donnée dans l'énonce.
Et lorsque x=-2 k(x)=-11

[Sa Majesté]

Non
Lorsque x=-2, x+2=0 et 1/(x+2) n'est pas défini

[Azzedine93]

Oui mais k(x) ce n’est pas que 2/x+2 c’est aussi 3x-5
On ne prend pas l’ensemble?

[Sa Majesté]

On ne prend pas l’ensemble?

Si justement
Puisque 1/(x+2) n'est pas défini pour x=-2, la fonction (3x-5)+(2/(x+2)) n'est pas définie pour x=-2

[Azzedine93]

D’accord merci beaucoup

[Azzedine93]

Y a-t-il une propriété ou une définition qui explique ceci?
Merci

[capitaine nuggets]

Salut !

Y a-t-il une propriété ou une définition qui explique ceci?
Merci

Cela vient du cours et plus précisément de la fonction "inverse"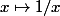 . Cette fonction est définie sur 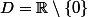car on ne peut diviser par , que si est non nul.

De manière générale, un quotient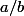 de deux réels et , est défini uniquement lorsque 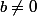, sinon cela n'existe : on ne peut pas diviser un nombre par . Du coup, la fonction est définie si et seulement si le dénominateur 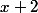est non nul, c'est-à-dire .

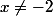Enfin la fonction "affine" est bien définie pour tout réel x, donc on en conclut que ta fonction est définie là où sont définies simultanément les fonctions et . La première est, on l'a vu, définie sur 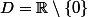et la seconde est définie sur 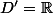donc le domaine de définition de est obtenu en effectuant l'intersection des domaines et 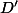: 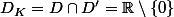(fait un dessin si besoin).

[Azzedine93]

Merci beaucoup je comprend mieux maintenant ! Mille merci