étude d'une fonction avec intégrale
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
lidwa852
- Messages: 4
- Enregistré le: 04 Fév 2020, 17:22
-
 par lidwa852 » 29 Fév 2020, 21:00
par lidwa852 » 29 Fév 2020, 21:00
Bonsoir,
j'ai commencé à faire le devoir maison ci-joint, mais je bloque sur la question 2)b) de la deuxième partie de l'exercice, merci pour votre aide
Montrer que pour tout

:
-ln(2) \leq \dfrac{ln(2x)}{x-ln(x)})
Voici mes calculs :
on a d'après la question 2)a) :
 = \int_x^{2x}\dfrac{dt}{t})
donc
 - ln(2) =\int_x^{2x}\dfrac{ln(t)}{t(t-ln(t))}dt)
En encadrant
}{t(t-ln(t))}dt)
avec
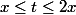
je tombe sur
}{2(2x-ln(x))} \leq F(x) - ln(2) \leq \dfrac{ln(2x)}{x-ln(2x)})
Pour la partie gauche on peut très simplement conclure que
}{2(2x-ln(x))})
Mais pour la partie droite je ne tombe jamais sur la forme voulue
Merci d'avance.

-
Rdvn
- Habitué(e)
- Messages: 840
- Enregistré le: 05 Sep 2018, 11:55
-
 par Rdvn » 01 Mar 2020, 11:11
par Rdvn » 01 Mar 2020, 11:11
Bonjour
2)b)
La fonction h est croissante sur l’intervalle [ 1 , + infini [
(première question)
La fonction que vous intégrez de x à 2x est définie par u(t) =ln(t) / (t.h(t))
Par manipulation d’inégalités , on obtient que pour tout t de [ x , 2x]
u(t) < ou = ln(2x) / (x .h(x)) et , sachant x<2x , on intègre cette inégalité pour
avoir la majoration souhaitée, à droite.
Je n’ai pas vérifié vos résultats, mais pour celle de gauche il suffit de remarquer
que u est positive sur [ x , 2x]
Bon courage
-
lidwa852
- Messages: 4
- Enregistré le: 04 Fév 2020, 17:22
-
 par lidwa852 » 01 Mar 2020, 15:29
par lidwa852 » 01 Mar 2020, 15:29
Ah oui, le problème c'est que je n'encadrais pas directement avec la fonction h et du je ne tombais jamais sur ce que je voulais
En tout cas merci beaucoup pour votre aide
Et à bientot
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 59 invités

