Tangente

[tommylebro]

Bonjour, alors voila, j'ai un exo où il faut que je trouve les valeurs ou la valeur de l'abscisse sur laquelle j'aurait une tangente avec un coef directeur égale à 0.25
Je connais l'expression de la fonction f(x)=4x/x+1
Pourriez me dire par où commencer, merci

[Flashtag]

Calcule la dérivée car le coef directeur de la tangente c’est la valeur de la dérivée puis tu résouts f’(x)=0,25

[tommylebro]

Merci mais comment je calcule la dérivée

[aymanemaysae]

Bonjour ;

Rappel : .

Tu as : et . Peux-tu donner : et ?

[tommylebro]

Bonjour, je suis en première et il me semble que cela est du terminale je n'ai donc malheureusement pas vu ça, y a t-il une astuce pour négliger cette formule et résoudre ce problème

[Flashtag]

Tu sais dériver des produits ou/et des puissances ?
Tu peux voir et deriver ça

[aymanemaysae]

As-tu déjà vu la notion de taux d'accroissement ?

[mathelot]

sinon, on a

(x+1)f(x)=4x

on peut dériver les deux membres de l'égalité en utilisant la formule de dérivée d'un produit
de deux fonctions dérivables (sur un intervalle ouvert I)

(uv)'=u'v+uv'

[tommylebro]

Oui j'ai déjà vu le taux d’accroissement, mais au niveau des formules et des dérivations de puissance j'ai pas vu ça en cours

[Carpate]

Je connais l'expression de la fonction f(x)=4x/x+1

Je crains que l'exercice n'aie pas de solutions car f(x) est le fonction constante x --> 5 de dérivée nulle !

[tommylebro]

Si il y a une solution, le coef directeur de 0,25 sera atteint en x=3 mais je sais pas comment y arriver

[GaBuZoMeu]

Carpate te fait remarquer que 4x/x+1 doit se lire, vu la priorité des opérations 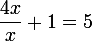(la division et la multiplication sont prioritaires par rapport à l'addition). Si tu veux écrire correctement et être compris sans ambiguïté, écris 4x/(x+1), avec la parenthèse bien placée

[aymanemaysae]

Si tu as vu la notion du taux d'accroissement , alors au point tu as : .

Tu as : et ;

donc :

.


Peux-tu , maintenant calculer : ?

[tommylebro]

J'avais fais ce genre de calcul et je trouvais à la fin : -4u² -4u + 8

[mathelot]

si tu connais la formule de dérivée d'un produit de deux fonctions et pas celle de dérivée d'un quotient:

pour tout x réel différent de -1:


les dérivées sont égales:

[titine]

J'avais fais ce genre de calcul et je trouvais à la fin : -4u² -4u + 8

Je ne comprends vraiment pas comment tu peux arriver à celà en calculant ton taux d'accroissement.
Reprends les calculs de aymanemaysae il a pratiquement tout fait ...
Attention, je ne trouve pas le même signe que lui ...

[aymanemaysae]

Tu as raison titine : j'ai corrigé ma faute de frappe . Merci !

[aymanemaysae]

up!


.

Le coefficient directeur de la tangente à au point d'abscisse est .

Il ne te reste plus qu'à résoudre l'équation suivante : .

[tommylebro]

Merci beaucoup ! J'ai bien compris grâce à vous

[aymanemaysae]

De rien et bonnes fêtes .