Montrer qu'un ensemble n'est pas majoré

[MathEtO]

Bonsoir,
Je cherche à montrer que l'ensemble n'est pas majoré.

Il est évident que G n'est pas majoré mais j'ai du mal à écrire une preuve correcte.

J'ai essayé en posant un majorant tel que pour montrer que ce majorant n'en est en fait pas un mais je n'arrive pas à conclure...

Merci d'avance pour votre aide.

[infernaleur]

Salut,
tu peux regarder la limite de racine de x.

[tournesol]

Une partie G de R n'est pas majorée veut dire par définition que pour tout M appartenant à R , il existe a appartenant à A tel que a>M .
Si M <0 , alors M<
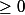
Si M , Il est immédiat que
Donc G n'est pas majoré .