The supplementary of a complex subspace of dim one
19 messages
- Page 1 sur 1
the supplementary of a complex subspace of dim one
we identify C^3 to R^6, ie $(z_1,z_2,z_3)=(x_1,y_1,x_2,y_2,x_3,y_3).$ Where x_i,y_i in R.$
Let H defined by:
H={(z_1,z_2,z_3)\in\ C^3/ z_1+z_2=0, z_3=0}
H is a complex subspace of complex dim one (i.e. real dim 2). As we can see
H=Span_R{ (1,1,-1,-1,0,0);(1,0,-1,0,0,0)}
Question: i want to find a supplementary H' of H in R^6. This supplementary will be of dimension four.
can any one help me to find Span of H'?
Let H defined by:
H={(z_1,z_2,z_3)\in\ C^3/ z_1+z_2=0, z_3=0}
H is a complex subspace of complex dim one (i.e. real dim 2). As we can see
H=Span_R{ (1,1,-1,-1,0,0);(1,0,-1,0,0,0)}
Question: i want to find a supplementary H' of H in R^6. This supplementary will be of dimension four.
can any one help me to find Span of H'?
Re: the supplementary of a complex subspace of dim one
bj,
réponse du badaud:
tu prends 6 vecteurs dans R^6 (dont les deux premiers)
et tu orthogonalise tout le monde avec Gram-Schmidt
réponse du badaud:
tu prends 6 vecteurs dans R^6 (dont les deux premiers)
et tu orthogonalise tout le monde avec Gram-Schmidt
la vie est une fête 
Re: the supplementary of a complex subspace of dim one
Bonjour, c'est ici un forum francophone. Tu devrais t'exprimer en français.
Tu peux prendre un supplémentaire de dans
dans  (facile à trouver) et le considérer comme sous-espace (de dimension 4) de
(facile à trouver) et le considérer comme sous-espace (de dimension 4) de 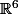 .
.
Tu peux prendre un supplémentaire de
Re: the supplementary of a complex subspace of dim one
pouvez vous m'aider s'il vous plait à le construire. d'autre part comment peut-on utiliser Gram-Schmidt.
Re: the supplementary of a complex subspace of dim one
Gram-Schmidt n'est pas une bonne idée : il faudrait partir d'une base, autrement dit on aurait déjà un supplémentaire.
J'ai déjà donné une indication, facile à mettre en oeuvre. Pour commencer, peux-tu décrire un plan -vectoriel supplémentaire de
-vectoriel supplémentaire de  dans
dans  ?
?
J'ai déjà donné une indication, facile à mettre en oeuvre. Pour commencer, peux-tu décrire un plan
Re: the supplementary of a complex subspace of dim one
normalement le supplémentairement suivant marche?
H'= {(z_1,z_2,z_3)\in\ C^3/ z_2+z_3=0}
H'= {(z_1,z_2,z_3)\in\ C^3/ z_2+z_3=0}
Re: the supplementary of a complex subspace of dim one
Oui, mais je croyais que tu préférais avoir un supplémentaire donné par générateurs plutôt que par équations.
Re: the supplementary of a complex subspace of dim one
oui on obtient par suite : H=vect{(1.0.0.0.0.0);(0.1.0.0.0.0);(0.0.1.0.-1.0);(0.0.0.1.0.-1)}
Re: the supplementary of a complex subspace of dim one
Un supplémentaire de H, tu veux dire, pas H.
Oui, c'est une possibilité.
Oui, c'est une possibilité.
Re: the supplementary of a complex subspace of dim one
bj,
via Gram-Schmidt,
pour une base de R^6, on peut prendre la canonique (représentable par matrice identité..que j'appèle I)
pour les deux vecteurs de H, h_1 et h_2. On orthogonalise h_2 contre h_1.
On récupère par exemple S = <[1,1,-1,-1,0,0], [0.5, -0.5,-0.5, 0.5,0,0]>
application de gramschmidt:
pour chaque vecteur e_i de I,
on orthogonalise e_i contre S aka o_i
si o_i est nul, alors o_i est combinaison linéaire de S, et on l'ignore
sinon on ajoute o_i à S
A la fin, si tout c'est bien passé, S contient 6 vecteurs (et non 8) et le supplémentaire est donné par les 4 derniers vecteurs de S
edit: le supplémentaire trouvé étant ici:
S_H = <[0.5,0,0.5,0,0,0]
[0,0.5,0,0.5,0,0]
[0,0,0,0,1,0]
[0,0,0,0,0,1]>
via Gram-Schmidt,
pour une base de R^6, on peut prendre la canonique (représentable par matrice identité..que j'appèle I)
pour les deux vecteurs de H, h_1 et h_2. On orthogonalise h_2 contre h_1.
On récupère par exemple S = <[1,1,-1,-1,0,0], [0.5, -0.5,-0.5, 0.5,0,0]>
application de gramschmidt:
pour chaque vecteur e_i de I,
on orthogonalise e_i contre S aka o_i
si o_i est nul, alors o_i est combinaison linéaire de S, et on l'ignore
sinon on ajoute o_i à S
A la fin, si tout c'est bien passé, S contient 6 vecteurs (et non 8) et le supplémentaire est donné par les 4 derniers vecteurs de S
- Code: Tout sélectionner
%https://www.maths-forum.com/superieur/the-supplementary-complex-subspace-dim-one-t210239.html
I = eye(6);
b = [
[1,1,-1,-1,0,0],
[1,0,-1,0,0,0]
];
function r=gramSchmidt(m,v)
r = v;
l = size(m,1);
for i = 1:l
u = m(i,:);
r -= (r*u')*u / (u*u');
end
end
b(2,:) = gramSchmidt(b(1,:), b(2,:));
for i = 1:6
col = I(i, :);
v = gramSchmidt(b,col);
if norm(v)>1e-10
% keep v
b(end+1, :) = v;
else
discardedVector = col
end
end
supplem = b(3:end,:)
checkortho = supplem*b(1,:)'
edit: le supplémentaire trouvé étant ici:
S_H = <[0.5,0,0.5,0,0,0]
[0,0.5,0,0.5,0,0]
[0,0,0,0,1,0]
[0,0,0,0,0,1]>
la vie est une fête 
Re: the supplementary of a complex subspace of dim one
D'accord tu pars d'un système générateur de 8 vecteurs et pas d'une base, ce qui permet d'éviter mon objection.
Il n'en reste pas moins que c'est vraiment marteau-pilon pour écraser une mouche, juste pour le plaisir d'écrire une procédure, n'est-ce pas ? Alors que la question se résout immédiatement et sans calcul.
On peut procéder comme l'a fait Jalled, On peut aussi voir que les vecteurs (1,0,0) et (0,0,1) complètent le vecteur générateur (1,-1,0) de H pour former une base de C³, ce qui donne immédiatement ((1,0,0,0,0,0) , (0,1,0,0,0,0),(0,0,0,0,1,0),(0,0,0,0,0,1)) comme base d'un supplémentaire dans R⁶.
Il n'en reste pas moins que c'est vraiment marteau-pilon pour écraser une mouche, juste pour le plaisir d'écrire une procédure, n'est-ce pas ? Alors que la question se résout immédiatement et sans calcul.
On peut procéder comme l'a fait Jalled, On peut aussi voir que les vecteurs (1,0,0) et (0,0,1) complètent le vecteur générateur (1,-1,0) de H pour former une base de C³, ce qui donne immédiatement ((1,0,0,0,0,0) , (0,1,0,0,0,0),(0,0,0,0,1,0),(0,0,0,0,0,1)) comme base d'un supplémentaire dans R⁶.
Re: the supplementary of a complex subspace of dim one
oui c'est ça. Merci pour vous pour la discussion. la question est bien résolu.
Re: the supplementary of a complex subspace of dim one
Un petit complément. L'exemple traité ici se résolvait à vue. Il peut donc être intéressant d'avoir une procédure qui calcule un supplémentaire dans des cas moins évidents. Mais ça me semble un mauvais choix d'utiliser Gram-Schmidt pour cette procédure, pour des raisons que je peux détailler.
Il existe par contre un algorithme "couteau suisse" pour les problèmes d'algèbre linéaire (sur n'importe quel corps) : l'échelonnement, ou pivot de Gauss.
Pour fournir un supplémentaire d'un sous-espace de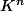 (
( un corps) donné par une famille génératrice :
un corps) donné par une famille génératrice :
1°) Échelonner la famille, ce qui fournit une base sympa du sous-espace.
2°) Compléter la base en piochant dans la base canonique les vecteurs qui bouchent les trous des pivots de la base échelonnée du sous-espace. Les vecteurs ajoutés forment une base d'un supplémentaire.
Il existe par contre un algorithme "couteau suisse" pour les problèmes d'algèbre linéaire (sur n'importe quel corps) : l'échelonnement, ou pivot de Gauss.
Pour fournir un supplémentaire d'un sous-espace de
1°) Échelonner la famille, ce qui fournit une base sympa du sous-espace.
2°) Compléter la base en piochant dans la base canonique les vecteurs qui bouchent les trous des pivots de la base échelonnée du sous-espace. Les vecteurs ajoutés forment une base d'un supplémentaire.
Re: the supplementary of a complex subspace of dim one
à part les flottants, je veux bien le détail de pourquoi pas gramSchmidt
je pense avoir une version via échelonnement:
qui est un code plus pénible à écrire...
je pense avoir une version via échelonnement:
- Code: Tout sélectionner
%https://www.maths-forum.com/superieur/the-supplementary-complex-subspace-dim-one-t210239.html
b = [
[1,1,1,1,1],
[1,1,1,1,1],
[1,1,1,2,3],
[1,1,1,2,0]
]';
suplem = []
%foreach canonical vector
start_vi=1;
for e_i = 1:size(b, 1)
%find pivot
found_vi = false;
for v_i = start_vi:size(b,2)
if b(e_i, v_i) ~= 0
found_vi = v_i;
break
end
end
if found_vi
%intervert columns
if found_vi ~= start_vi
old = b(:, start_vi);
b(:,start_vi) = b(:, found_vi);
b(:,found_vi) = old;
end
%make zeros on the right
for v_i = start_vi+1: size(b,2)
if b(e_i, v_i) ~= 0
f = b(e_i, v_i) / b(e_i, start_vi);
b(:, v_i) -= f*b(:,start_vi);
end
end
start_vi += 1;
else
v = zeros(size(b,1), 1);
v(e_i) = 1;
suplem(:,end+1) = v
end
end
b
suplem
#output
b =
1 0 0 0
1 0 0 0
1 0 0 0
1 1 0 0
1 2 -3 0
suplem =
0 0
1 0
0 1
0 0
0 0
qui est un code plus pénible à écrire...
la vie est une fête 
Re: the supplementary of a complex subspace of dim one
Mes raisons sont :
1°) L'échelonnement (pivot de Gauss) est, comme je l'ai écrit, un couteau suisse pour les problèmes d'algèbre linéaire. On a intérêt de toutes façons à l'avoir dans sa panoplie.
2°) Gram-Schmidt est limité aux calculs sur les réels, ou sur les complexes si on prend garde à la conjugaison pour le produit scalaire hermitien. Il ne fonctionne pas sur les corps finis par exemple. On peut se dire qu'on s'en fiche, sauf que l'algèbre linéaire sur les corps finis a une sacrée importance pour les applications (ne serait-ce que pour les codes correcteurs d'erreurs).
Tu ne seras peut-être pas sensible à ces arguments, mais pour moi ils sont importants. Point de vue temps de calcul, il n'y a pas de différence flagrante entre LU (pivot) et QR (Gram-Schmidt) :

1°) L'échelonnement (pivot de Gauss) est, comme je l'ai écrit, un couteau suisse pour les problèmes d'algèbre linéaire. On a intérêt de toutes façons à l'avoir dans sa panoplie.
2°) Gram-Schmidt est limité aux calculs sur les réels, ou sur les complexes si on prend garde à la conjugaison pour le produit scalaire hermitien. Il ne fonctionne pas sur les corps finis par exemple. On peut se dire qu'on s'en fiche, sauf que l'algèbre linéaire sur les corps finis a une sacrée importance pour les applications (ne serait-ce que pour les codes correcteurs d'erreurs).
Tu ne seras peut-être pas sensible à ces arguments, mais pour moi ils sont importants. Point de vue temps de calcul, il n'y a pas de différence flagrante entre LU (pivot) et QR (Gram-Schmidt) :

Re: the supplementary of a complex subspace of dim one
Tu ne seras peut-être pas sensible à ces arguments, mais pour moi ils sont importants.
un petit côté France Gall ?

ok, effectivement je suis pas trop sensible vu que j'ai encore moins eu à travailler avec autre chose que R (le corps), donc oui peut être si jamais ça arrive un jour je me souviendrai du pivot...
A force de voir du sage, peut-être finirai-je enfin par l'installer!
la vie est une fête 
Re: the supplementary of a complex subspace of dim one
Je suis très surpris que tu négliges le pivot de Gauss. L'échelonnement, c'est vraiment la clé de beaucoup d'algorithmes d'algèbre linéaire (inversion de matrice, calcul de déterminant). C'est aussi l'outil fondamental de l'algèbre linéaire sur les entiers (forme normale de Hermite).
Re: the supplementary of a complex subspace of dim one
C'est pas une question de négligence, c'est pas même une question de préférence, j'ai pas eu besoin, je m'en sers pas.
Si t'as un marteau mais rien a clouer, ben tu t'en sers (normalement) pas.
Par curiosité, j ai regardé hermite, succintement, pour resoudre une eq diophantienne "lineaire" parce que t'as donné le mot clé, sinon j'aurais meme pas envisagé qu'on puisse employer l'échelonnage pour
Si t'as un marteau mais rien a clouer, ben tu t'en sers (normalement) pas.
Par curiosité, j ai regardé hermite, succintement, pour resoudre une eq diophantienne "lineaire" parce que t'as donné le mot clé, sinon j'aurais meme pas envisagé qu'on puisse employer l'échelonnage pour
la vie est une fête 
19 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 64 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
